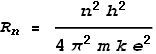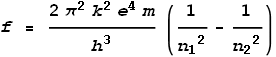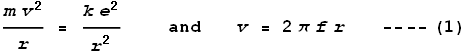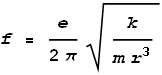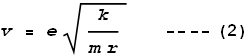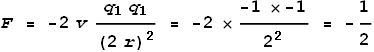Atomic Orbits
The nature of atoms and the manner in which electrons interact and move about their
nucleus has puzzled scientists for a long time. What ought to be a simple orbit of
electrons around a nucleus has been complicated by the fact that electrons appear to group
themselves at certain fixed altitudes, while occasionally radiating light at particular
frequencies. Various models of the atom have been forwarded in an attempt to explain the
anomalies. They range from simple planetary models, to standing particle-waves, to
probability distribution functions whose precise physical nature confounds the
imagination.
In earlier chapters we studied the nature of the electromagnetic force in much detail and
discovered that this force has unexpected properties when charged particles are in motion.
These include properties such as a ‘sideways force’ which moves particles
non-directly. Could the proposed modifications to Coulomb’s force law provide any
insight to the behaviour of atoms? Here we investigate that possibility.
The Rutherford model
A brief history lesson is appropriate. In 1911 Ernest Rutherford studied
experiments involving bombarding atoms with alpha-beams. They showed that most of an
atom’s mass was positively charged and packed into a small volume. From this he
developed a planetary model of the atom which proposed that electrons orbit a heavy
positive nucleus; much like planets orbit the Sun. Prior to this it was believed that the
nucleus was large and electrons were imbedded within: the so-named ‘plum pudding
model’.
Rutherford’s model was intuitive. One could easily imagine a
miniature solar system with the electrostatic force substituted for gravity. But the model
had some problems. First, an electron orbiting a proton would radiate energy and this,
according to energy conservation laws, would require it to steadily lose altitude; causing
it to spiral into the nucleus. Second, electrons could orbit at any altitude and radiate
any frequency. This was inconsistent with observation.
The Bohr model
Enter Niels Bohr, who in 1913 proposed a model of the atom based on the
idea that electrons behave as waves. In this model electron waves would surround the
nucleus in a standing wave formation. The wavelength of an electron was said to be based
on its velocity and, seeing that velocity was also based on distance from the nucleus, it
followed that electrons could only orbit at certain fixed radii.
By combining orbital mechanics, Coulomb’s law, and the recent work of
Planck, Bohr calculated the orbital altitudes of electrons in a hydrogen atom should be:
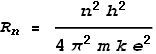
Where n is an integer number greater than zero, Rn
is the nth radius, and e, k
and h are the standard universal constants: electron charge, Coulomb and
Planck. Bohr’s model predicted a shell structure of the atom where n
represents the shell number. A value of n=1 represents the shell nearest
the nucleus. It is called the ‘Bohr radius’ and has a value of 5.29x10-11
m. This is close to the empirical (measured) radius of a hydrogen atom: 2.5x10-11
m.
Knowing the radius, he could also determine the velocity and kinetic energy of an electron
at each shell. Bohr went farther to state that when an electron moves between shells it
emits radiation, and the energy of this radiation will correspond to the difference
between these energy levels. This energy can then be divided by Plank’s constant to
determine frequency. It yields:
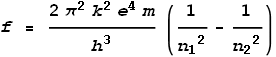
Where n1 and n2
are positive integers corresponding to shells, with n2>n1.
This formula amazingly matched the observed frequencies that were emitted by excited
hydrogen gas, and even more amazingly, it predicted frequencies outside the visible
spectrum that had not yet been discovered.
The fact that Bohr’s model gets the frequencies right strongly indicates that
it’s close to reality. Bohr was definitely on to something! Yet there are some
problems with his model:
According to this model, when the electrons orbit the nucleus they
don’t emit radiation. Realistically we should expect the same emission problem as
with Rutherford’s model. This lack of emission suggests the electron isn’t
moving. Yet the calculation for Bohr’s radius is based on centrifugal force and
‘particle-wavelength’, both of which require velocity.
The model says that when electrons jump between shells they emit a
photon of single frequency. Single frequency means a pure sine wave. Producing pure sine
electromagnetic waves requires oscillating a charged particle, e.g. an electron, in a sine
wave motion – at least that’s how it works for radio transmission. But an
electron jumping between shells is unlikely to do so in a sine wave fashion. Instead, the
radiation we would expect from a jumping movement is a ‘step function’ which
corresponds to multiple frequencies.
Finally (to state the obvious problem) the model doesn’t explain
why electrons should move as waves.
The origin of emissions
To gain a better understanding of the atom, a good first step may be to
look at how these single frequency emissions are occurring. Bohr claims they are generated
when electrons jump between shells. Yet as pointed out above, such a movement would
produce only a ‘blip’ in the electric field, not a sine wave.
We know that producing a pure frequency in the radio portion of the electromagnetic
spectrum requires oscillating electrons in a sine wave motion; e.g. within an antenna.
Thus it seems reasonable to assume that producing pure frequencies in the visible portion
of the spectrum requires oscillating an electron at a visible-light frequency. Are there
any electrons oscillating within an atom? There sure are! How about the orbital motion of
an electron around the nucleus? When viewed from the side, an electron orbiting a proton
in a circle would appear as a sine wave. In fact it would appear as a sine wave from every
direction. Could this orbital motion be the true origin of sinusoidal waves?
We know from experiment that the radius of a hydrogen atom is approximately 2.5x10-11
m. If an electron were to orbit at that distance, at what frequency would it do so? Taking
the rule that Coulomb force should cancel centrifugal force, and the relation between
frequency and velocity, namely:
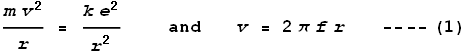
we get frequency as:
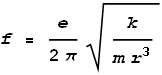
Substituting the measured radius we determine a frequency of 2x1016
Hz, which corresponds to a wavelength of 15 nm – a wavelength in the high ultraviolet
range. The observed hydrogen emission spectrum is typically in the range of 95 –
1000+ nm. Admittedly the calculated value of 15 nm is somewhat outside this range; yet not
terribly far out. A problem may be that the measured radius was taken from a hydrogen
molecule, which emits no radiation. It will be shown further on that the hydrogen which
emits radiation has a different form and thus the above calculation would only be
approximate in this case.
Based on the above reasoning I would like to suggest that these fixed frequency emissions
are not caused by electrons jumping between shells, rather, they are caused by electrons
orbiting a nucleus at fixed altitudes.
Formula (1) also allows us to determine the velocity as:
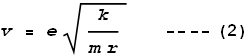
Using the measured radius this gives a velocity of 3.2x106 m/s,
which is about 1% of light speed. This information will be relevant further on. |
A Simple Hydrogen Atom
Following in Bohr’s footsteps came Schrödinger and Heisenberg, who
postulated that electrons move according to wave functions that describe a probability
distribution around the nucleus. Given that these models lay outside the classical realm,
I’ll not attempt to analyse their validity. Instead I’ll propose a new model of
the hydrogen atom.
Based on the Velocity Dependent Coulomb’s Law (VDCL) and sideways forces, this is how
an electron will orbit a proton:
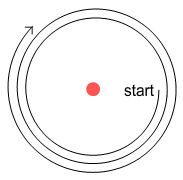
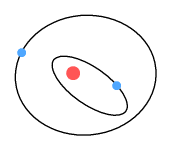
Here we see the electron is spiralling away from the proton. Why is this?
Refer to the chapter on the sideways force. When an
electron moves past the proton, force lines pass through it at an angle. This causes the
electron to receive a gentle push in its direction of motion; causing it to steadily
spiral away from the proton.
Critics of the Rutherford model claim the electron should spiral inward. The reason for
the inward direction is due to energy loss and the requirement of energy conservation. But
the motion of an electron is not controlled by a desire to satisfy energy conservation
laws. The only thing that can make an electron move is force. And the only force that
could cause it to spiral inwards is a retarding force against its direction of travel.
Critics of the model make no suggestion of what that force could be.
Nonetheless we know that an isolated hydrogen atom is unstable and this indicates its
orbiting electron must either spiral in or away from the proton. Given that an inward
spiral would involve releasing high-frequency radiation (as the spiral velocity
increased), and we don’t see this, it seems more likely that it spirals out.
Furthermore an inward spiral would likely end with some sort of sub-atomic/nuclear
particle interaction when the electron meets the proton, and we don’t see this
either.
Hydrogen in a static field
It happens that there is a way of making our above hydrogen model stable,
and that is to place it within a static electric field. The field here will be net-neutral
as shown below.

On the left is a hydrogen atom consisting of a proton and electron. On the
right is a positive and negative charge of equal but opposite value. These are far enough
away to make the field approximately parallel. When we set the electron in motion an
interesting thing happens. See below.
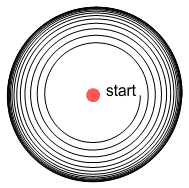
As before, the electron starts spiralling away from the proton. It then
reaches a point where the orbit radius stops enlarging and becomes fixed in size.
What has happened here? Due to the VDCL, as the electron moves right it feels increased
repulsion from the negative charge and decreased attraction from the positive charge.
Conversely as it moves left, attraction increases and repulsion decreases. The net result
is a retarding force over the orbit period.
When the electron was close to the proton it felt a promoting sideways force which pushed
it away. But as it got further away, this force weakened and the retarding force from the
distant charges took over. At some point these forces became equal and the orbit remained
steady.
If the electron instead starts outside this orbit it spirals inward and arrives at an
(almost) identical orbit:
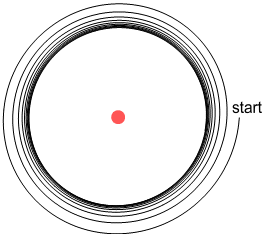
This is very interesting because it shows that charged particles outside
the atom can cause an electron to settle into a steady orbit at a fixed distance from a
nucleus. Here the radius of orbit depends on the amount of charge in the exterior
particles: increasing their charge reduces the radius and vice-versa. So this is not
really a fixed orbit like what Bohr might predict, but the above scenario does provide
some clues as to how an orbit could become stable.
A Simple Hydrogen Molecule
One of the odd things about the development of atomic models is that fact
that scientists always start by attempting to model the hydrogen atom. The reason this is
odd is that it is well known by scientists that singular hydrogen atoms don’t exist,
other than very briefly. Ironically, the fact that the Bohr model predicts a stable
hydrogen atom is proof that the model must be wrong!
Instead hydrogen only becomes stable when joined to another atom; most commonly to another
hydrogen atom in forming a H2 molecule. Using the VDCL and sideways force
interactions, is it possible to arrange a pair of hydrogen atoms into stable molecular
formation? How about this:
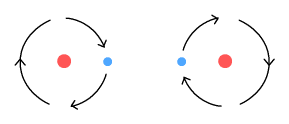
Above we see two hydrogen atoms side-by-side with their electrons orbiting
in mirrored but opposite directions. This arrangement solves several problems at once:
1. No emissions.
When the electrons are orbiting in opposite directions, each radiates a sinusoidal signal
that is the opposite of the other. The two signals cancel each other out, and will do so
when observed from any direction. In this way the molecule emits no net signal (no light).
2. No outward spiral
As the electrons pass by each other they create a retarding sideways force. Much like the
external charged particles described above, this prevents the orbits from becoming
increasingly larger, i.e. from spiralling out.
3. A covalent bond
This arrangement shows how a covalent (molecular) bond may be formed. When the electrons
are at the far outer positions, the protons repel each other. Then when the electrons are
near the mid section, each proton feels attraction toward the electrons. When these two
forces balance the protons end up separated at a fixed distance, forming a covalent bond.
Covalent bonds are often described with the term ‘electron sharing’ which
implies that each electron spends time orbiting both protons. It’s important to note
however that, while the electrons here do influence each other’s orbits, they only
orbit their own proton, i.e. there is no sharing of electrons as such.
4. Fixed distance of orbit
With the protons at a fixed distance, this in turn fixes the orbit radius of the
electrons. The electrons will settle into equilibrium when the promoting sideways force of
the protons matches the retarding sideways force of the electrons. Here we see
‘quantum mechanics’ come into play.
A Hydrogen emission model
The hydrogen molecule described above emits no radiation. This matches the
normal situation we observe with unexcited hydrogen gas. What about the situation where
excited hydrogen emits radiation, and does so at discrete frequencies? There may be a way
of explaining this also.
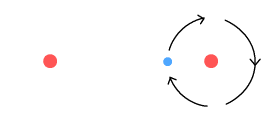
Above we see a hydrogen molecule in which the leftmost atom has lost its
electron, perhaps as a result of being heated and colliding with another molecule. It
might be supposed that the isolated proton should also break away at this point. But it
will be held in place due to the fact that when the remaining electron is midway it
creates an attractive force between the protons.
The other thing this isolated proton can do is to keep the remaining electron from
spiralling out. Due to the VDCL, the electron will feel a greater force moving away, than
moving toward, the isolated proton. The result is a net retarding force which will keep
the electron orbiting at a certain altitude. While in orbit, the electron will radiate a
single frequency, possibly within the visible spectrum.
In the above diagram we note there are two degrees of freedom: the distance between the
protons and the distance between the electron and its proton (the orbit altitude). We
might suppose that there are only a certain number of possible distance solutions that
satisfy an equilibrium situation involving a circular orbit and stable covalent bond.
These solutions might correspond to the frequencies we observe in the hydrogen spectrum.
Naturally the above is speculation and confirmation will require a proper analysis (to be
done later).
A Simple Helium Atom
Next in the periodic table comes helium. Unlike hydrogen, helium is stable
on its own and has no molecular form. Is it possible to construct a helium model using
similar methods? How about this:
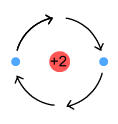
Above is a nucleus containing two protons (charge=+2). It is surrounded on
either side by electrons that are opposite each other and following the same circular
orbit in clockwise fashion. Each electron emits a sine wave, but as the waves are 180
degrees out of phase, they cancel each other’s signal. As a result no radiation is
emitted.
This model is useful from the point of view of cancelling radiation. Unfortunately it has
a number of problems:
1. If this works for helium then it should also work for hydrogen, namely, it should be
possible to place two electrons either side of a single proton. This would yield a
negative hydrogen ion. Coulomb’s inverse square law tells us the opposing force
between electrons will only be a quarter of the attractive force from the proton. So there
is no problem force-wise. But we don’t observe negative hydrogen ions.
2. The model only works if the electrons are exactly opposite each other and moving with
equal speed. Any deviation from this will cause one electron to eventually move under and
eject the other electron.
3. The most significant problem has to do with sideways forces. The promoting sideways
force from the protons will cause electrons to spiral outward. This model intends to
counteract that by making the electrons impose a retarding sideways force on each other.
The electrons are further away but have the advantage of moving at twice the relative
velocity. Will it be enough?
Formula (2) above tells us that the velocities we are dealing with are around 1% of light
speed. According to the earlier chapter on sideways
force, at low velocities this force will be proportional to velocity and
Coulomb’s force.
Let the velocity of an electron be 1, its charge be -1, and distance from the nucleus be
1. The nucleus (2 protons) then has a charge of +2 and a velocity of 0. The promoting
sideways force from the proton then will be (setting c=1 and k=-1
for convenience):
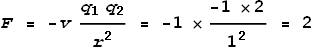
The electrons have a distance of 2 and relative velocity of 2. The
retarding sideways force between them will be:
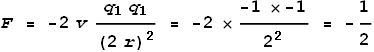
As can be seen, the promoting sideways force is many times greater (4
times) than the retarding force. Hence the electrons will spiral out. If this model fails
for helium, it would fail to an even greater degree with larger atoms, e.g. a lithium ion
(Li+). In fact it also fails for hydrogen. Obviously we need a different model.
The Helium Atom, take 2
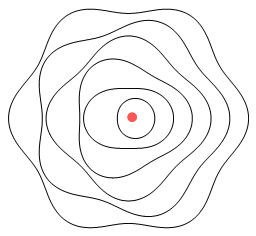
Okay then, here’s another helium model:
Here the electrons have elliptical orbits and orbit in opposite
directions. Each electron takes turns at being near the nucleus. The electron that is
farther from the nucleus still feels a net attractive force due to there being two protons
to attract and only one electron to repel. Because they move in opposite directions, the
electrons exert a retarding sideways force on each other and this overcomes the
promotional sideways force from the nucleus.
One good thing about this model is that it will work no matter how many protons are in the
nucleus. Another other good thing is that it won’t work with hydrogen. This
is because a single proton can’t overcome the force from a closer low-orbit electron.
Hence no negative hydrogen ions are allowed, just as in reality.
A problem however is that the electrons won’t properly cancel each other’s
signal. When viewed from above or below the electrons are moving in opposing directions so
there is an opportunity for them to cancel. But when viewed from the front or side, the
electrons are moving in the same direction. Hence a signal will be emitted. This is a
problem because we don’t observe emissions from helium.
One unusual property of helium is that it’s impossible to freeze; at normal pressures
at least. Even when cooled to absolute zero it remains liquid. No other element behaves
this way. Could the reason for this be that helium atoms are constantly being interrupted
by the emissions of other helium atoms? Since no emissions emerge from helium gas or
liquid, this suggests that an emission from one helium atom is being absorbed/cancelled by
the counter-emission of another. This would cause constant motion amongst helium atoms,
preventing them from solidifying.
Unlike other inert gases, helium doesn’t have additional electrons to absorb the
emissions from the two electrons in its inner shell. Nor can it form a covalent bond with
another atom, such as the hydrogen molecule described above in which two atoms cancel
signals directly.
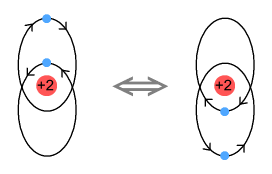
But there is one method of making helium solidify and this involves placing liquid helium
under pressure. Placing liquid helium under pressure might force the atoms to arrange in
face-to-face & upside-down pairs in which they would fully cancel each other’s
emissions. At this point the atoms can remain still and form a solid. This pressure would
be required because of helium’s inability to form covalent bonds.
Conclusion
It may be possible to explain the nature of atomic orbits using classical
methods and without resorting to the notion of particle waves. Using the VDCL we can
account for the behaviour of hydrogen in both its elemental and molecular form; both in
terms of its spectral emission and forming of a covalent bonds. We can also account for
some properties of helium.
The models described here are incomplete without a proper analysis of electron motion and
prediction of observed spectra. But this will have to wait until we analyse the
atom’s nucleus.
To be continued. |