The Speed of Gravity
If our Sun were suddenly to cease to exist would Earth immediately
break from its orbit and move in a straight line or would it spend the
next eight minutes circling a non-existent star?
The answer to this depends upon whether you consider the effects of
gravity to be instantaneous or delayed. If gravity propagated
at infinite speed, Earth would immediately break from its orbit, and
this would be despite us seeing sunlight for the next 8.3
minutes. But if gravity propagated at a finite speed, such as
the speed of light, Earth would continue along its orbit path for as
long the Sun remained visible.
According to mainstream belief, gravity moves at light speed, meaning
that its effects will be delayed. But there’s a competing
school of thought that argues gravity must either move at infinite
speed or at a speed much-much faster than light. The reason
for proffering this is that planetary motion requires it for our Solar
System to be stable.
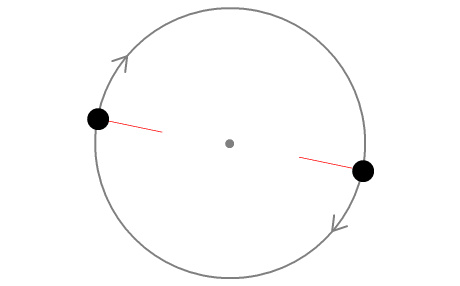
The argument goes like this. Suppose we have two identical
bodies orbiting each other in a perfectly circular orbit as shown:
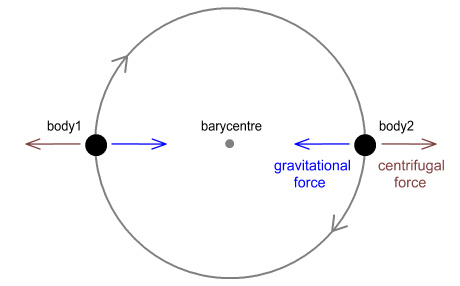
They orbit clockwise around a barycentre that’s in the exact
middle. There are two forces at work. The first is
the gravitational force pulling them together and the second is the
centrifugal force pulling them apart.
In order to retain their perfect circular orbit it is necessary for
these forces to be equal in magnitude, opposite in direction, and
perpendicular (at right-angles) to the direction of motion.
If the directions were not like this the bodies would either spiral
inwards or outwards.
But why would the force directions not be opposite?
Whenever making predictions about gravity, it is often assumed to be
instantaneous, which is to say it is assumed to travel at an infinite
speed. The above diagram also makes this assumption and has
the direction of gravitational force pointing directly back at the
other body.
But if gravity moved at finite speed this wouldn’t be
correct. Because in the time it took for gravity to reach the
other side, the body that emitted the gravity would have moved
forward. Instead, each would see an earlier image of where
the other one was. This diagram shows the idea:
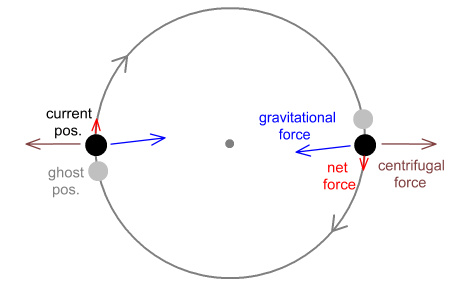
Here each body sees a ‘ghost image’ of the other body, where the
‘ghost’ corresponds to an earlier location. This suggests the
gravitational force must be coming from that location rather than the
location of where the other body currently is. So the
centrifugal force will still be directly outward but the gravitational
force will be at a slight angle. This means there will now be
a net force very mildly in the direction of travel. This will
cause the bodies to spiral slowly outwards:

In the case where the bodies are of unequal mass, both bodies will be
orbiting a shared barycentre and the problem would still
occur. Thus we should likewise expect the Sun and Jupiter to
spiral apart, followed by the other planets, leading to the Solar
System’s destruction.
Tom Van Flandern
This argument was put forward by the late Thomas Van Flandern and can
be found here [1]. Based on this he calculated that, in order
to explain the Solar System’s stability, gravity must propagate at at
least 2x1010c, i.e. 20 billion times faster than
light. And for all we know it may well propagate at
infinite speed allowing it to act instantaneously over any distance.
If gravity really does move that fast it offers exciting opportunities
for faster-than-light communication. On the other hand it
also seems unbelievable; especially the idea that it could be
instantaneous.
Two Archers
But there’s a fault with the above reasoning in that it fails to take
into account the motion of the body emitting the gravity.
This can be demonstrated as follows.
Two archers stand on opposing sides of a rotating turntable.
Each has a bow and arrow and is trying to hit the other
archer. Initially they aim directly at where their opponent
is standing as shown:
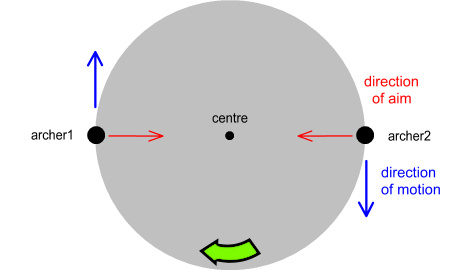
The turntable is rotating clockwise. If the archers release
their arrows with this aim they face two problems. The first
is that when the arrow arrives at the other side, the target will have
moved. The second is that the person firing the arrow is
moving sideways and this motion will be applied to the arrow.
The end result will be this:
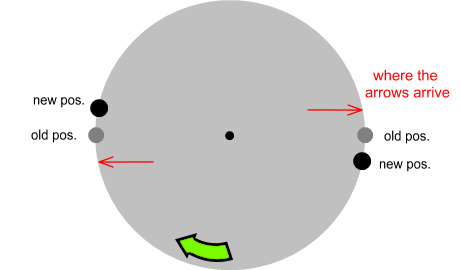
Not only do the arrows miss their target, they also miss the location
they were aimed at.
In order to compensate for this, each archer must aim to his right as
shown:
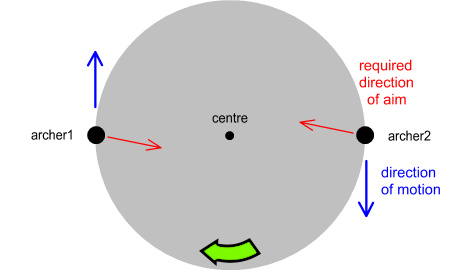
When the arrows are released, they will hit their target like this
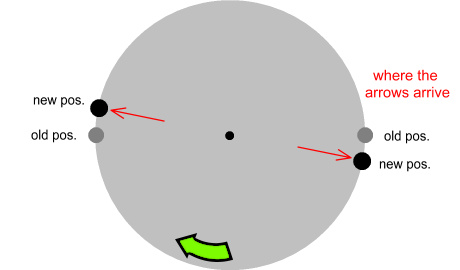
Notice how the arrows point back at the archer that fired them.
Now suppose the arrows applied a force to their target and the force
direction was along the line that the arrows were pointing.
The archers would feel a force aiming directly away from where they now
saw their opponent. And this would be despite both of them
having moved from the spot where the arrows were fired.
Now let’s apply this idea to the original gravity scenario:

Here we see gravity represented as lines radiating from the
bodies. The gravity radiates equally in all directions but
only one pair of lines end up hitting the targets. Those
lines are shown in red.
A short while later the gravity hits the opposing bodies.
Both bodies have moved from their original locations. But
just like the arrows, the red field lines point directly back at the
originating bodies’ new locations.
Unlike arrows, gravity exerts an attractive force. So the net
result is a force pointing back at the originating body, and this
happens despite there being a delay in the transmission. The
inward force direction is now directly opposite to the centrifugal
force and the bodies will not spiral apart after all.
We can apply the same principle to bodies of non-equal mass, such as
the Earth-Moon system. In this case the bodies will move at
different speeds with the heavier body moving more slowly and closer to
the barycentre. The below diagram shows the equivalent
situations with archers:
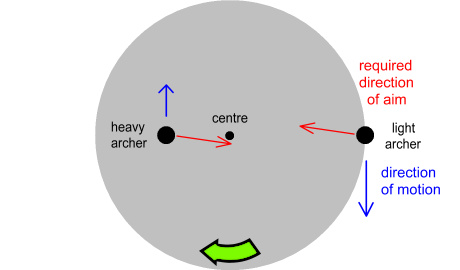
Here the ‘heavy’ archer stands closer to the centre of the turntable
which represents the barycentre of their ‘orbit’. But even
though their speeds are different (relative to the barycentre), each
will use the same angle of aim to hit their target.
Applying this logic to a gravitational situation gives the same
result. Namely that the gravitational force will point back
to the originating body, as though gravity had crossed the space
between them at infinite speed, even if it hadn’t.
Bradley Aberration
Another reason put forth for why gravity might apply a force in the
direction of a body’s motion is Bradley aberration. In 1727
astronomer James Bradley observed that the location of stars appeared
to shift in the direction that Earth moved around the Sun.
This diagram shows the idea:
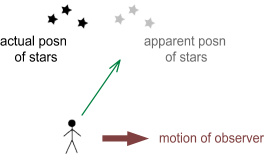
It was also noted that the angle the stars were at corresponds to v/c
where v is the speed of Earth around the Sun.
If light changes its incoming direction to match tangential velocity,
perhaps gravity does likewise? And perhaps as we orbit the
Sun we should also experience gravity at an angle of v/c?
Not necessarily. In order to answer this we need to
look at what is causing the aberration. A likely cause of
Bradley aberration is that light is hitting the molecules in the
atmosphere more on one side than on the other. This diagram
shows the idea:
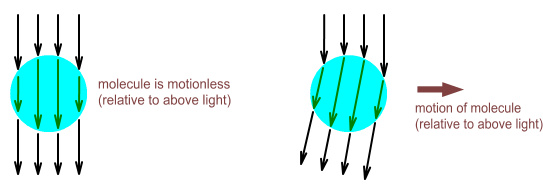
The left image shows a molecule as motionless, relative to an above
light source. The light hits the top surface of the molecule
equally and gets transmitted directly downward. In the right
image the molecule is moving to the right. The light hits the
right side of the molecule more than the left. As a result
the light is then transmitted at an angle.
Applying this to the atmosphere as a whole, this is most likely what is
occurring:
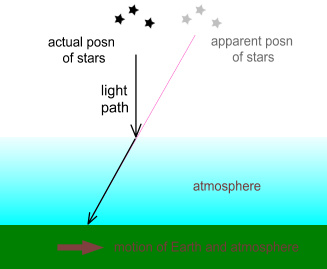
Light strikes the atmosphere directly from above but then gets
transmitted through the atmosphere at an angle. This makes
the stars appear to be in a different location. Actually this
would occur even if there were no atmosphere because the light
would strike a telescope lens or eyeball with a tangential velocity and
be transmitted through it at an angle.
So Bradley aberration is likely an optical phenomenon similar to
refraction. We know that light has a number of behaviours
when interacting with material. It can bounce off mirrors,
bend through mediums, and diffract through openings. But we
never observe gravity doing these things. So there is no
reason to believe Bradley aberration should necessarily apply to
gravity.
Further observations on the nature of gravity
What the above tells us is that a slow gravitational speed doesn’t
necessarily mean that an orbit will be unstable. Gravity
might move at an infinite speed but that is highly implausible since
that would mean its effects would be instantaneous over unlimited
distances. It is also unlikely that it moves at the 2x1010
times faster than light suggested by Van Flandern.
If the above reasoning is correct and gravity does move at a finite
speed and without pointing at a ‘ghost image’ of an attracting body,
this tells us something about the nature of gravity:
- That it is radiated at a fixed speed relative to its
source rather than to an observer or hypothetical background aether.
That is, if gravity moves at speed g (relative to its source) and the
source were moving at speed v (relative to an observer), the speed of
the gravitational field relative to the observer will be g+v.
- That the orientation of the field – i.e. the angle it was
emitted at – is important and is preserved within the field.
- That the direction of force will be along the direction
that the field was emitted at rather than the direction it impacts a
target body.
This diagram shows how gravity acts along the orientation it was
emitted at rather than the direction the field is moving at:
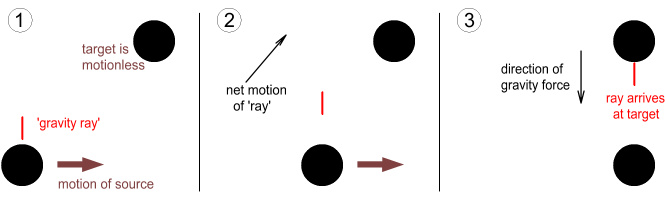
Here we see a target body standing motionless and a source moving to the right.
In the first frame the source emits a ‘gravity ray’. The ray moves
directly away from the source whilst also pointing directly away. In the
second frame the ray is halfway to the target and is moving at a diagonal
relative to the target. In the third frame the ray arrives at the target.
Despite it hitting the target at an angle, it applies a force directly
downward.
Conclusions
The stability of the Solar System cannot be used as proof for gravity
being infinite in speed or moving at a large multiple of light-speed.
Bradley aberration is probably an optical effect having to do with
light hitting transparent mediums at an angle and is not applicable to
gravity.
[1]
http://www.ldolphin.org/vanFlandern/gravityspeed.html
|













