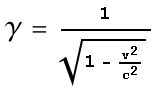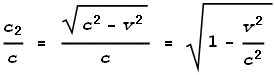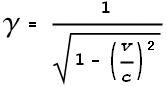The Lorentz Transform

In the discussion of Special Relativity (SR), an equation known as the Lorentz Transformation appears on a regular basis. This equation, also referred to as the Lorentz-Einstein Transformation, is used to determine a number of variations in physical attributes that take place when an object moves at near light speeds. It has the form:

Where v is velocity of an object, c is the speed of light and γ is a multiplier factor that can be applied to attributes such as distance, mass and time. In this chapter I will give a derivation for the Lorentz Transform. This is a more entertaining derivation than what’s commonly found in science texts but it uses the same vector calculations and thus yields the same results.

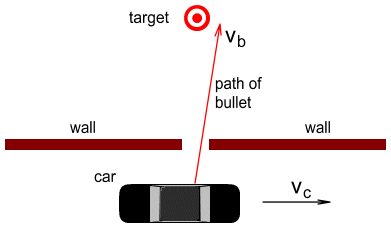
The Hit Man’s Dilemma

Suppose that a crime gang had a problem that needed solving. The ‘problem’ was in the form of a competitor from a rival gang and ‘solving’ it required the services of a hit man. Now it so happened that this competitor did not make himself easily accessible and only ventured out at a certain time of every day for a smoke. He stood at the front of a building that was protected from the main road by a brick wall with an opening in it. See below diagram.

car shooting at target

The hit man decided that the only way to do the job was via a drive-by shooting. But he had three problems to surmount:

1. It was a busy road and he couldn’t stop the car to make the shot.
2. Because of the wall, he could only shoot while directly opposite the target.
3. If he aimed at the target, the car’s forward movement would cause the bullet to miss (see red line above).

So the only way to hit the target would be to aim the gun slightly to the left to compensate for the car’s forward movement. Let v_c be the velocity of the car and v_b be the velocity of the bullet (as measured relative to the gun). To hit the target, the gun will need to be angled such that the left-horizontal component of the bullet is equal to the velocity of the car. See below diagram.

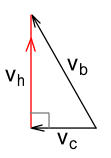
hitman vector diagram

Here we can see that while the bullet moves at full speed relative to the car, it will hit its target at slightly less than full speed. Let v_h be the velocity at which the bullet hits its target. Using pythagoras we see that:

$v_h = \sqrt{v_b{}^2-v_c{}^2}$

In other words the hit speed v_h will steadily decrease as the car’s velocity v_c increases, and will become zero when the car moves as fast as the bullet.

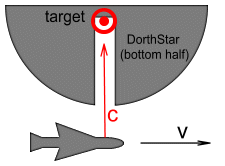
A Star Wars Dilemma

Now fast forward to the future. Our hero Lube Skystalker has been sent on a mission to destroy the evil DorthStar planet. For this mission he will need to fly past the planet’s entrance and shoot a powerful laser beam into its innards. See below diagram.

starship hitting target

Lube faces the same challenge as the hit man in the earlier example, namely that he will need to compensate for his space-ship’s forward movement in order to aim the beam at the target. Let v be the velocity of the ship and c be the speed of the light from the laser gun. How fast will the laser beam hit its target? Using the same method as with the previous example we get:

$c_2 = \sqrt{c^2-v^2}$

Where c₂ is the velocity of the light at the target.

Now here’s where SR comes knocking at our door. According to SR, the light speed at the target must be the same as at the source, not less than c. In order for this to happen the time-sensation at the target must be slower than at the source. How much slower? To adjust the time-sensation we first need to consider the ratio of c₂ and c:

$\frac{c_2}{c} = \frac{\sqrt{c^2-v^2}}{c} = \sqrt{1-\frac{v^2}{c^2}}$

This ratio can be used to multiply the time-sensation of the target so that it will perceive the beam to be moving at the normal speed of light. This factor, or rather its inverse (for some reason it’s expressed in the reciprocal form), is known as the Lorentz Transform factor γ namely:

$\gamma = \frac{1}{\sqrt{1-\left(\frac{v}{c}\right)^2}}$

From the above equation we can see that γ has a value of one when velocity is zero, and moves toward infinity as velocity approaches the speed of light. For example when the velocity is 50% of light speed, γ has a value of 1.15; at 90% of light speed, γ has a value of 2.3; and at 99.5% of light speed, γ has a value of 10. This means that at 50% the time-sensation at the target will be 13% slower; at 90% it will be 2.3 times slower and at 99.5% it would be 10 times slower than the source.

The Lorentz transform equation demands that the velocity of an object cannot reach light speed and cannot exceed it. This limitation on speed is a fundamental requirement of SR.