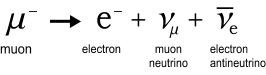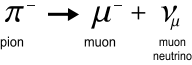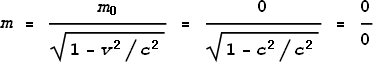Particle Physics
For the longest time as history records, science has held that all matter is composed of
fundamental building blocks. Even though they could not see it, the ancient Greeks for
example presumed that a stone could be ground up into finer and finer grains until it
reached single indivisible points of matter which they called átomos, meaning
“uncuttable”. Their suspicions proved correct, as some two-and-a-half-thousand
years later scientists in the early 20th century discovered that indivisible
unit and named it the atom.
This naming turned out to be premature as it was later found these atoms could be further
broken into smaller particles, namely the proton, neutron and electron. But that was not
the end of the tale. Over the following decades particle accelerator experiments revealed
there to be large number of, what were labeled, sub-atomic particles. This gave birth to a
new branch of science called particle physics.
Developmental Problems
As time passed and more and more particles were discovered, it became
clear that something was amiss with these ‘fundamental’ units of nature. Their
numbers ran into tens then to over a hundred. Could nature be this complicated? A study of
their properties and interactions led to the idea that many of these were made up of still
smaller units. This led to the discovery of quarks, which are said to compose protons,
neutrons and other particles.
While it is true that a large number of particles might pose a philosophical problem, a
more fundamental problem must be the way in which they are said to interact. In the world
of particle physics, matter is constantly flashing in and out of existence as new
particles are created and destroyed. And while this process may seem strange, it is
stranger still that many of these interactions appear to occur without regard to mass
conservation. Take muons for example.
Muons
Muons are charged particles that are primarily generated as a result of
cosmic bombardment in the upper atmosphere. They are mostly negatively charged and can be
thought of as heavy but unstable electrons. Muons have a short half-life of 2.2
microseconds, after which they decay into an electron and a couple of neutrinos. The decay
process goes like this:
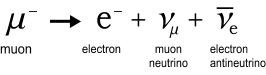
This reaction obeys the charge conservation rule in that both muon and
electron have an equal negative charge while the neutrinos are neutral. But a muon is 206
times heavier than an electron and the neutrinos weigh nothing (or next to nothing). Where
did all that mass go? According to modern physics, mass must either be conserved or
converted to an equivalent amount of energy, determined via the E=mc2
relation. This energy must be released in the form of electromagnetic radiation, i.e. as
photons. But there is no suggestion in the standard texts that photons are released during
this process.
Actually, the above diagram is incomplete because there should also be a W–
boson particle involved. This W– particle weighs in at 157 thousand
times heavier than an electron and quickly flashes in-and-out of existence while creating
the electron and one of the neutrinos. Here again is another apparent violation of mass
conservation, and a huge one at that! But since it quickly disappears we could give it the
benefit of doubt and say that it causes no overall conservation problem.
One possibility for mass conservation may have to do with neutrino momentum. I will
discuss this further on.
Pions
The next question has to do with where muons come from. Muons come from
pion decay, which in turn are generated from high-energy proton collisions in the upper
atmosphere. The pion to muon conversion process looks like this:
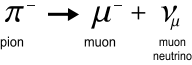
Again there is a temporary intermediate W particle
involved which I’ve not shown. The pion has a mass of 273 electrons which is only
slightly above the muon (at 206) and there are no photons in sight. Hence again we have a
mass conservation problem, albeit only minor. Ignoring the various neutrinos then, the
complete process goes something like this:

Notice something amiss? That’s right: the positive proton yields a
negative pion! This is surely impossible according to charge conservation rules. Now to be
fair, the interaction is not stated in full like this. Various literatures on the subject
discuss the pion/muon and muon/electron decays separately and each decay process shown
preserves charge correctly. But when it comes to the full process the literature becomes
somewhat vague, particularly in regard to the pion’s charge. For example on
Wikipedia’s muon page we find the following [1]:
When a cosmic ray proton impacts atomic nuclei of air atoms in the upper atmosphere,
pions are created. These decay within a relatively short distance (meters) into muons (the
pion's preferred decay product), and neutrinos.
The above excerpt does not say what charge these pions have except they are somehow
created from protons. Since protons are positive this indicates the created pions must
also be positive, in which case they could not decay into negative muons. The webpage from
SLAC helps clear this up when it says [2]:
In cosmic ray showers, both muons and antimuons are produced about equally.
That’s good. With equal amounts of muons (negative) and antimuons (positive), charge
is conserved. But where are all these antimuons? If they are produced in equal numbers and
have equal half-lives, we should observe them equally at sea level. Instead the literature
indicates a vast abundance of muons.
An explanation of pion/muon conversions
The above raises many questions. Does the cosmic proton convert directly
to pions or does it create the pions as part of a collision, while preserving its own
existence? And what happened to all that mass? Did the mighty cosmic proton convert itself
to a puny electron without releasing the required amount of radiation to account for mass
difference?
Given the uncertainty over the charge conservation problem in pion creation, it is
understandable that the available literature is somewhat vague on details. However I
believe there is a better explanation for the above reactions that not only preserves
charge and mass, but also does away with these mysterious particle disappearance and
creation-out-of-nothing conjectures.
Start with the proton. As was discussed in the chapter on nuclear
forces, a proton is believed to be made up of two up-quarks (positive) and one
down-quark (negative). Is it possible that these quarks are really the pions and muons we
observe? I.e., is the negative muon really a down-quark and the positive pion an up-quark?
According to scientists, protons are essentially unbreakable and quarks can never be seen
on their own. But this seems unlikely. If a proton is made of several parts, and you hit
it hard enough, e.g. in a high-energy cosmic collision, then surely those parts would
separate. Scientists have declared that quarks have fractional charges and, given that
we’ve never seen a fractional charge, we’ve obviously never seen a broken
proton. This idea of fractional charges was initially introduced to explain the
composition of the neutron purely in terms of quarks. But as pointed out in the previous chapter, neutrons can be more easily explained in
terms of a proton joined to an electron. Could it be that quarks in fact have unit charges
and have been hiding in plain sight all along?
With this idea in mind, let’s assume our proton has just smashed into some part of
the atmosphere, e.g. a nitrogen nucleus, and has split into three quarks: two positive and
one negative. What now? Refer to the chapter on matter-energy
conversion. There it was postulated than an electron and positron can overlap,
creating an effectively invisible composite particle, which I called a poseltron. Could a
similar event be happening here? The positive quarks are surrounded by electrons. They
could quickly absorb one each and become an ‘invisible’ neutral particle. The
pions have apparently decayed!
But the down-quark is negative and cannot absorb electrons so it continues down. This is
the muon we see. What will happen to it – will it absorb a positron and also
disappear? Perhaps, but this is unlikely because there are few positrons to be had;
they’ve already been absorbed by available electrons and become poseltrons.
Here’s instead what happens. The high-velocity muon collides with a poseltron. This
causes the electron-positron pair to split. The positron is absorbed into the muon and the
electron is ejected. Voila! The muon ‘decayed’ into an electron. Of course the
muon is still there but as it’s now overlapping a positron, it forms a particle of
neutral charge and can no longer be seen.
Here’s the full process in picture form:
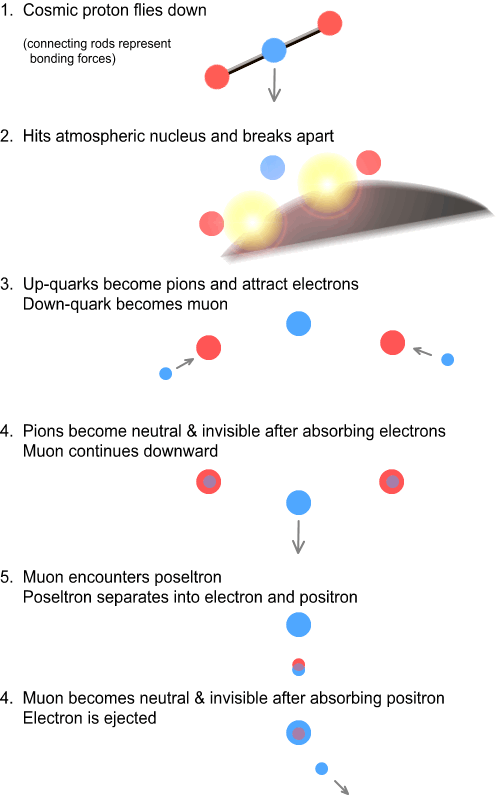
As can be seen, no fundamental particles have been created or destroyed, while charge and
mass are conserved throughout.
Some points on pion/muon lifespan and mass
The pion has a much shorter lifespan than a muon: about 85 times shorter
(0.026 vs. 2.2 microseconds). Based on the above, that’s to be expected. Electrons
are everywhere and will quickly be absorbed by a pion. But poseltrons and positrons are
rare. Hence a pion will only last a few hundred metres before being absorbed, whereas a
muon can often make it all the way to sea level.
If a muon is really a down quark this means a down-quark weighs around 206 electron
masses, i.e. about one ninth of a proton. Since there are also two up-quarks in a proton
this means that an up-quark should weigh (1836-206)/2 = 815 electron masses. There’s
a problem here because a pion reportedly weighs only 273 electron masses. So either
I’m way out on the assumptions or there’s something fishy about the way a
pion’s mass is measured.
Neutrinos
Now some discussion needs to be made about neutrinos because I’ve
ignored them in the above interactions. Neutrinos are neutral particles emitted during
certain decay processes such as neutron decay and the pion and muon decays described
above. They have a mass of zero or, according to recent speculations, very close to zero.
The existence of neutrinos was first postulated by Wolfgang Pauli in 1930 to explain why
electrons leaving a nucleus in the form of beta radiation move more slowly than expected.
They were later observed/confirmed in bubble chamber experiments.
That a neutral particle could be observed however comes as a startling claim. By any
interpretation of Coulomb’s or Maxwell’s laws, a purely neutral particle (i.e.
containing no charges) could not apply any force on a charged particle, nor could it be
affected by a static or electromagnetic field. An answer to this may be that they can be
observed when impacting another particle directly. The below image shows the bubble
chamber experiment in which a neutrino was first detected [3].
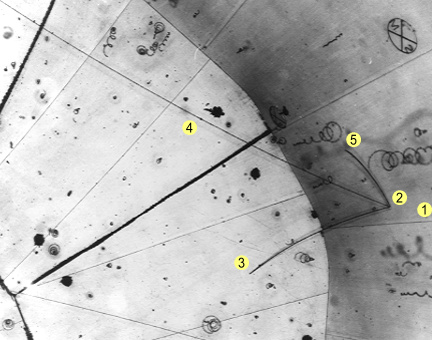
The accepted interpretation of this is: (1) a neutrino came in from the
right (it can’t be seen due to having no charge). (2) It hits a proton. (3) A
positive pion is produced and curves downward. (4) A negative lighter muon is also
produced and moves quickly to the left, curving weakly upward. (5) The original heavier
proton survives; it moves slowly and curves downward.
According to the standard particle physics model, when oppositely charged particles meet
they should annihilate. Apparently the rules are different for neutral particles; namely
that they should bounce off other particles like billiard balls, and this requires
sub-atomic particles be slightly elastic. Assuming this is true, how can we calculate the
degree of elastic bounce? In any classical situation this would be easily solved in terms
of momentum and energy conservation. Knowing the momentum requires knowing the mass and
this is a problem because neutrinos are commonly assumed to have none.
Special relativity tells us that particles having zero mass, such as photons, must travel
at light speed. This is due to the relativistic mass formula, which says an object’s
mass increases toward infinity as it nears light speed. For an object of non-zero mass
this puts the brakes on acceleration and keeps v below c.
But for an object with zero mass the acceleration can only stop when the particle hits
light speed, at which point the object gains a non-zero relativistic mass. What will this
mass be? To determine this we can use the Lorentz Transform equation:
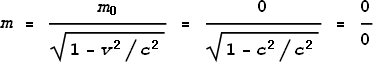
Where m0 is the rest mass.
In mathematical terms, zero divided by zero is called an indeterminate, meaning that it
can have any real-number value, or even an infinite one. Calculating momentum requires
multiplying this indeterminate mass by velocity, in this case c, which of
course just gives us another indeterminate. This is not helpful!
But could a neutrino with indeterminate mass/momentum account for the mysteries it is said
to solve, such as muon/electron mass-loss and the collision in the above image? After all,
if it’s indeterminate then we can assign any value we want to it, right? Perhaps, but
we’d be hard-pressed to explain why identical objects moving at the same velocity
have different relativistic masses. After all, the speed of light is a universal constant;
not a universal variable.
So if neutrinos don’t account for the above collision what does? Here’s my
interpretation. The invisible particle coming from the right (1) is actually a positive
pion and negative muon overlapping (similar to the poseltron concept). It strikes the
proton (2) and this causes the pion and muon to break apart and become visible. The three
particles, pion, muon and proton (3,4,5 respectively), are then scattered.
A far more interesting aspect of this image arises from measuring the extent of
scattering. A simple pixel measurement shows the length of each track to be:
| Proton |
72 |
| Pion |
155 |
| Muon |
>442 |
This scatter distance represents velocity which, due to momentum
conservation, should be inversely proportional to mass. From this we see the pion has
approximately half the mass of the proton. A ratio of the pion/proton track lengths gives
72/155 = 0.465. Now see the paragraph farther up where I
speculated that an up-quark weighs 815 electron masses. Taking the ratio of up-quark to
proton mass we get 815/1836 = 0.444. That’s very close to the pion/proton ratio!
Hence it’s quite likely that a pion is an up-quark after all.
In the muon’s case, it ended up off screen so I can only calculate a ratio of 442/72
= 6.1, which is understandably less than the real muon/proton ratio (about 9) because the
track must be longer. But seeing as the muon’s mass has already been determined in
other experiments by comparing its particle tracks to electrons, we can accept their
stated mass as being 206 electrons.
Neutral composite particles
This description of a pion-muon particle (which struck the proton in the
above image) as well as the poseltron spoken about in the earlier
chapter gives rise to the possibility that there are many neutral composite particles
in existence. Here are some charged particles we commonly know of:
| Negative |
Positive |
| Electron |
Positron |
| Muon |
Antimuon |
| Pion- |
Pion+ |
Looking at this table we see there are nine ways that positive and
negative charges could combine to make a neutral particle. The electron-positron pair has
been discussed already and it is worth considering the evidence for other combinations.
One possible combination is the ‘neutral pion’.
The neutral pion (symbol pi0) is a type of pion having no
charge. It has a very short half life of 8.4x10-17 seconds and decays into two
photons. According to the literature, this pion is made of four quarks: up, down, anti-up
and anti-down. By comparison the charged pions are made of only two quarks each. Despite
having twice as many quarks, the neutral pion is somehow lighter than a charged pion: 264
versus 273 electron masses. Again we have another mass conservation problem, and this
indicates the assumed particle composition is incorrect.
Here is another interpretation of its decay process. The neutral pion is made of two
opposite charges particles. The electric field from a passing photon temporarily forces
them apart. They quickly come back together. In the process they oscillate through each
other and create electromagnetic waves (photons) similar to the poseltron oscillation process. If we know the frequency of
these photons this would give a clue as to the particle’s masses and allow us to
determine which particles were involved. Based on the abundance of particle types, the
most likely candidate would be a positive pion and negative muon, i.e., an up/down-quark
combination.
A Bold Hypothesis
In the above description of muon to electron conversion, the muon decayed
when it met a poseltron. This caused the electron and positron to separate, followed by
the muon absorbing the positron and ejecting the electron. Here is a diagram showing a
break-down of events:
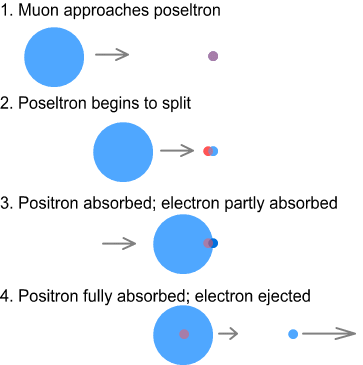
The electron and positron are pictured smaller than the muon because they
are lighter. If we assume sub-atomic particles to be made of a similar material of uniform
density, this would make the muon/electron diameter ratio proportional to the cube-root of
their mass ratio: in this case making the muon about 6 times larger as shown.
The idea that there should be direct correlation between mass and size seems quite logical
and this is probably how most would view sub-atomic particles. But this view alas creates
a problem for the electron-positron separation shown above. If the electron was much
smaller than the muon its charge density would be much higher. Hence the muon would be
unable to force the electron and positron to separate because the electron would be using
a much higher percentage of its charge to attract and hold the positron. The only way the
above could work is for the muon and electron to be very similar in size.
Based on this reasoning I’d like to make a bold hypothesis:
All fundamental (indivisible) sub-atomic particles are identical in size. They vary
only in mass and charge.
If this is true, everything from an electron to a top quark has the same diameter but
different densities. This may turn out to be true only for certain types of particles such
as those in the pion/muon/electron interactions. But if this principle can be
extended to all particles, it would allow for a much broader range of interactions. Hence
many composite particles could be composed from a small number of fundamental particles.
Conclusions
The conversion of cosmic protons into electrons, via pions and muons, can
be understood in terms of particle absorption. In this manner no decay or creation of
matter is involved and mass is preserved.
The existence of neutrinos is not required to explain particle interactions. If such
particles do exist, they would have no effect on matter and be undetectable.
Protons are breakable. The up and down quarks that make up a proton are in fact positive
pions and negative muons respectively. Quarks, like other particles, have unit charges;
not fractional ones.
It’s possible that all fundamental particles are identical in size.
[1] http://en.wikipedia.org/wiki/Muon
[2]
http://www2.slac.stanford.edu/vvc/cosmicrays/cratmos.html
[3] http://en.wikipedia.org/wiki/File:First_neutrino_observation.jpg |