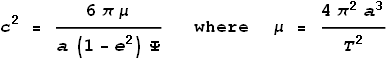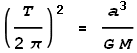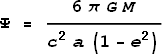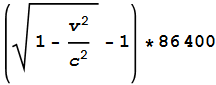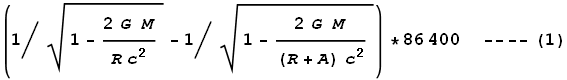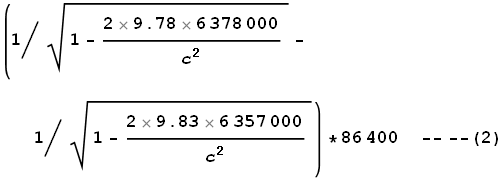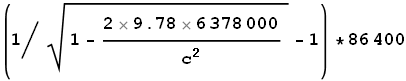General Relativity Experiments

In the preceding chapter we looked into the fundaments of General Relativity Theory (GR), and identified a number of contradictions within it. Just like Special Relativity (SR) however, GR has a number of experiments to confirm its contentions.

Some of them are:
. Light bending
. Gravity Lensing
. Perihelion of Mercury
. Clocks on GPS satellites

There are other experiments also but we’ll focus on the above since these cover the important elements of GR.

Light bending

The first item of evidence involves a famous experiment to determine whether gravity is able bend light, such as from stars.

First some background. To be precise, the idea that gravity could bend light is not entirely the domain of GR. We know from classical mechanics that an object moving through a gravitational field will do so in a curve. The degree of curvature is based only on speed and not on its mass. Therefore we could hypothesise that an object with zero mass, such as a photon, should also curve and its degree of curvature will be based on its speed: c. With GR however, the degree of curvature calculates to double this amount.

On May 29, 1919 an astronomer named Arthur Eddington took photos during a solar eclipse. The photos showed that stars close to the Sun appeared further out than they should be. This showed that the light from the star had somehow curved around the Sun and changed the apparent positions of the stars. Given that light might bend from a Newtonian perspective however, Eddington’s mission was not just to determine if gravity could bend light but whether it did so according to Newtonian or GR predictions. Eddington predicted a GR curvature of 1.75 arc-seconds, versus a Newtonian prediction of 0.87. He then measured a curvature of 1.61; a result which gave weight to the GR prediction and was heralded as a proof of GR.

Now it is frequently charged in academic circles that Eddington’s experiments were faulty. Particularly that: (a) his equipment wasn’t accurate enough to measure the predicted arc-second angular differences (b) the experiments were done during mostly cloudy weather, and (c) he threw out the photographs that didn’t confirm GR postulates [1].

Whether Eddington did so or not however is probably not very relevant now because since then the experiments have been apparently reproduced on several occasions. Does this mean that gravity does bend light after all, and to a degree predicted by GR? Or could there be another explanation?

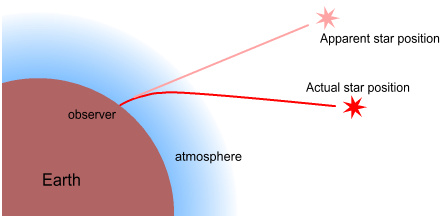
In olden times, before GPS, seafaring navigators would turn to the stars. By looking at, e.g. the angle of the North Star above the horizon, they were able to calculate their latitude above the equator. Now it was well known then as it is now that the observed position of a star is not its actual position. The reason is that Earth’s atmosphere refracts/bends light and causes stars to appear at higher elevations. This is shown below.

The Earth is not the only planet with an atmosphere. Venus, Mars, Jupiter, Saturn, etc., also have atmospheres. In fact, every object in the Solar System with large enough gravity appears to hold an atmosphere. The Sun is far larger. Does it have an atmosphere? It sure does! The atmosphere of the Sun, also called the corona, is visible and extends many millions of miles into space.

Doesn’t it seem likely then that this atmosphere would also refract the stars around it, causing them to appear at higher ‘elevations’ much as they do on Earth? If the Sun had an atmosphere, regardless of what gasses composed it, light from stars would have no ‘choice’ but to refract through it as shown below.

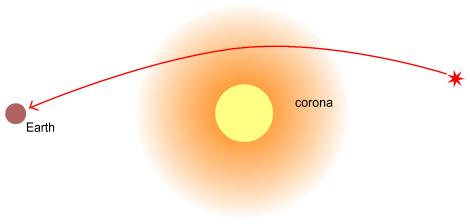
So how do we know that this bending of light is nothing other than refraction through an atmosphere? One objection to this idea might be that the stars are above the corona and thus couldn’t be refracted by them. But the corona is just an illuminated portion of the atmosphere. Beyond the corona would likely be further gasses albeit less dense and not illuminated. After all, the Earth’s atmosphere doesn’t stop suddenly at some altitude; it just steadily becomes thinner. There is no reason to assume why the Sun wouldn’t do likewise.

A further objection might be that the light bending may be a combination of both refraction and gravity. This is a possibility certainly, however in order to confirm this it would be necessary to account for both of these effects in the measured total. As far as can be determined, Eddington didn’t do so, nor do more recent experiments make mention of the possibility.

Gravitational lensing

Beyond the Solar System a related phenomenon is occurring. It involves the bending of light around stars and large celestial bodies such as galaxies and galaxy clusters. The bending of light around all sides of these bodies can cause them to act like cosmic magnifying glasses. This is called gravitational lensing and allows astronomers to view larger images of the objects behind them (behind the celestial bodies, not the astronomers).

But if the Sun has an atmosphere then stars and other giant bodies must be likewise surrounded with gas. In fact formations called nebulae are known to be made up almost entirely of dust and gas. Therefore it stands to reason that these bodies should likewise refract light around them, leading to a magnifying effect. If refraction is the true cause of the gravitational lensing phenomenon then it would seem more appropriate to call it ‘gas lensing’.

There is one aspect of gravitational lensing however that’s quite different from the visual effects observed during solar eclipses. Namely, gravitational lensing can cause light to be bent or stretched into arcs. There are a number of curious aspects to this phenomenon that are too deep to go into here, but I discuss them in a supplemental chapter:

Abell 1689 - Analysis of gravitational lensing (<-- click to read)

Perihelion of Mercury

One of the earliest and most accurate items of evidence supporting GR theory has to do with the planet Mercury. Unlike most planets, Mercury has a strongly elliptical orbit about the Sun. Its orbit isn’t fixed however; instead the elliptical path steadily rotates forward. An exaggeration of the pattern looks like this:

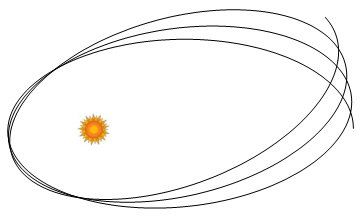
Precession of Mercury's perihelion

As each orbit is completed the new orbit begins at a point slightly in advance of where the previous orbit began. This is known as "the advancement of the perihelion of Mercury". The reason the perihelion (the point in the orbit of a planet nearest to the Sun) advances has to do with a number of things, one of which is the influence of other planet’s orbits.

Using Newton’s gravity equations, we can determine that the predicted advancement in the orbit should be 532 arc-seconds per century. The measured advancement however is 575 arc-seconds: 43 more than predicted. In 1915 Einstein used GR to calculate the expected amount of precession using GR and found the calculation yielded a precession of 43 arc-seconds, which precisely accounted for the difference.

The work of Paul Gerber

Step back in time. Two decades earlier a German physicist named Paul Gerber was exploring the same subject. Gerber proposed that the speed of gravity was the same as light and this might account for the missing precession. In 1898 he published a paper "The Space and Time Propagation of Gravity" [2]. See an English translation here. In this he calculated the speed of gravity to be very close to light speed.

Toward the end of the paper it states light speed as:

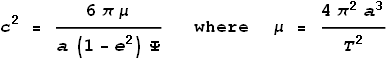
$c^2 = \frac{6 \pi \mu }{a \left(1-e^2\right) \Psi }\text{ where }\mu = \frac{4 \pi ^2 a^3}{T^2}$

Where a is the semi-major axis, e is the eccentricity, Ψ is the perihelion advance and T is the time of an orbit.

Kepler’s third law of planetary motion tells us that:

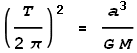
$\left(\frac{T}{2 \pi }\right)^2 = \frac{a^3}{G M}$

We can substitute T into the above formulae and give the precession as:

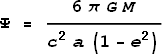
$\Psi = \frac{6 \pi G M}{c^2a \left(1-e^2\right)}$

Where G = 6.673x10^-11 N m² kg^-2, M (mass of sun)= 1.989x10³⁰ kg, c = 2.998x10⁸ m/s, a = 5.791x10¹⁰ m, e = 0.2056.

Substituting these values gives a precession of 5.019x10^-7 radians per orbit. Multiplying this by 415.2 (orbits per century) and then by 3600*180/pi (converting to arc-seconds) we get 42.98 arc-seconds per century - an ideal match to observation!

In other words, using only Newtonian gravitation plus the reasonable assumption that gravity propagates at light-speed, Gerber calculated the correct result. Given that classical mechanics can fully account for the missing precession, in what way can we say that the precession proves GR theory instead of Gerber’s calculation? Here there is no need for the relativity calculation. It is also important to note that Gerber’s paper was published 17 years before the GR papers and thus developed independently of GR.

This doesn’t mean that Gerber’s method is correct either, just that there is more than one way of getting the required amount. A more important question is, is the actual descrepancy 43 arcseconds? A careful analysis indicates otherwise and is discussed in a supplemental chapter:

Mercury’s Perihelion Advance (<-- click to read)

Clocks on GPS satellites

Another strong piece of evidence used in support of GR is the Global Positioning System (GPS). GPS satellites are said to experience a net time dilation of 38,700ns (nanoseconds) a day: +45900ns due to GR and -7200ns due to SR [3].

As explained in an earlier chapter, any time dilation experienced by the satellites won’t affect the accuracy of GPS receivers because the receivers determine their local time from the satellites’ clocks. But that aside, time dilation effects will show up in a comparison between satellite clocks and ground-based atomic clocks. We will examine this here by looking closely at the SR and GR numbers.

The amount of dilation due to SR can easily be determined using the LT. Plugging the satellites’ orbit velocity of 3780m/s into the LT and multiplying by the number of seconds per day gives: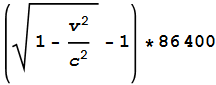

$\left(\sqrt{1-\frac{v^2}{c^2}}-1\right)*86400$

This equals -7.2x10^-6 seconds or -7200ns and agrees with the stated amount. So far so good. Now to calculate dilation due to GR.

The satellites orbit at an approximate altitude of 20,200km. Using equation (3) in the chapter on General Relativity we can calculate the expected differences in time dilation at the Earth’s surface and at the satellite:

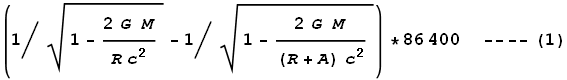
$\left.(1\left/\sqrt{1-\frac{2 G\text{ }M}{R c^2}}\right.-1\left/\sqrt{1-\frac{2 G\text{ }M}{(R+A) c^2}}\right.\right)*86400\text{ ----}(1)$

Where M is the mass of Earth, R is the radius, A is the altitude of the GPS, and 86400 is the number of seconds in a day. Substituting values of M=5.974x10²⁴, R=6.357x10⁶, and A=2.02x10⁷ we get:

Net dilation = 45850 ns.

And this closely matches the measured amount. Brilliant!

Relativity on the Earth’s surface

Before dissecting the above result, let’s look at a related question that has to do with relativity (both types) on the Earth’s surface: Given that the equator is in constant motion relative to the poles, is there any time dilation between the two? Put another way, should atomic clocks run at different rates at the pole and equator?

Since the equator is moving, SR would predict that clocks on the equator run slower. However, since the equator has lower gravity, GR would predict them to run faster. Which clock wins the race? To answer this we must calculate the amount of dilation of each type.

First the SR. The velocity at the equator is 465.1 m/s. For this speed, the Lorentz factor gives a value of 1+1.203x10^-12. Over a 24 hour period this would make clocks on the equator run 104ns slower.

Now the GR. Earth’s gravity measures at 9.78 m/s² at the equator and 9.83 m/s² at the poles. It has a radius of 6,378 km at the equator and 6,357 km at the poles. Using equation (2) in the chapter on General Relativity we can calculate the expected differences in time dilation over a 24 hour period:

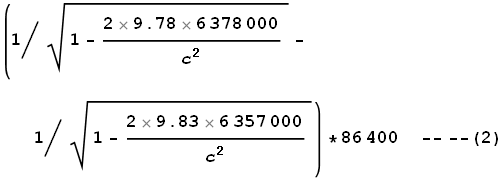
$\left(1\left/\sqrt{1-\frac{2 9.78 6378000}{c^2}}\right.-1\left/\sqrt{1-\frac{2 9.83 6357000}{c^2}}\right.\right)*86400\text{ ----}(2)$

This comes to 108ns.

These two values almost cancel each other out meaning that the clocks will tick at the same rate. Actually the clocks should completely cancel due to equipotential of the Earth’s surface as shown at this site [4], but we are lacking enough numerical precision to make the values equal.

No equivalence for GPS

The fact that SR & GR cancel across the Earth’s surface is a mixed blessing. On one hand it’s good because we don’t need to worry about unsynchronized clocks at different latitudes. On the flip side it means that we can’t use them to verify relativity. But there is a reason for pointing this out and that has to do with the Equivalence Principle.

We know that gravity at the equator is made of two components: actual gravity from the Earth (a downward pull), and centrifugal (upward) force which lessens the effect. We can easily calculate the strength of the centrifugal component to be 0.034 m/s².

In above equation (2) the quoted value of gravity at the equator, 9.78 m/s², is the measured value. The true equatorial gravity must be 9.780+0.034=9.814 m/s². However we don’t use this true value of gravity in our calculation of GR time-dilation, only the net (real gravity minus centrifugal force) value. The reason for this has to do with the Equivalence Principle which states that gravity and acceleration are indistinguishable and should be treated alike. If we used the number 9.814 we would calculate a gravitational dilation at the equator that is higher than at the pole – the opposite of what we need to counteract SR at the equator.

Now cast your eye to our earlier calculation of GPS GR time dilation shown in equation (1). Here we determined the difference between dilation at the equator and dilation at the satellite. The first term, with R in denominator, represents time dilation at the equator. The second, with R+A, represents dilation at the satellite. Let’s split these apart:

Time dilation at equator is:
1 + 6.9774x10^-10

Time dilation at satellite is:
1 + 1.6702x10^-10

The first term represents the gravity at the equator. The second represents gravity at the satellite. Is something amiss here?

Hang on a tick... gravity at the satellite? There’s no measurable gravity on man-made satellites! The satellite is in orbit and experiences an outward force exactly equal to the inward real-gravitational pull. The net gravity, according to the Equivalence Principle, is therefore zero and the satellite shouldn’t experience gravitational time dilation.

So what should the net dilation between the equator and satellite be? Using the above equation (2) with the second term set to 1 (for zero dilation), we get:

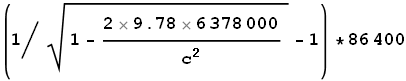
$\left(1\left/\sqrt{1-\frac{2 9.78 6378000}{c^2}}\right.-1\right)*86400$

= 59960 ns

This value is 31% higher than the quoted value of 45900ns.

A GPS fudge?

What does this mean? Why is it that when calculating the GR dilation on Earth we take into account centrifugal force, basing calculations only on ‘net gravity’, while on GPS satellites we ignore centrifugal force? Put another way, why doesn’t the Equivalence Principle apply to GPS?

According to the U.S. Naval Research Laboratory, experiments done during the initial testing of GPS satellites in 1977 showed that unadjusted satellites overall ran faster than Earth-based atomic clocks by 442.5 parts in 10¹² [5]. This equates to an inaccuracy of 38230ns per day [6] – a close fit to the SR+GR calculations shown above.

However these calculations are inconsistent with the Equivalence Principle as used in comparisons between pole & equator clocks. If the same logic was applied to both sets of clocks, the net dilation for GPS satellites would be 59960-7200 = 52760ns : 37% higher than the stated value of 38600ns. Why the difference?

Is it possible that ... GPS satellites experience NO dilation at all ?

Keep in mind that prior to the invention of satellites there was no easy way to test the SR and GR postulates properly. Up to this point the evidence was shaky, the errors large, and hence much of GR and SR was just assumed to be correct. What would happen then, when GPS was being developed, if the engineers discovered that in fact no dilation occurred?

Information like that would be pretty embarrassing, especially to the mainstream scientific community who had been preaching relativity for the past 70 years. What to do? Admit they’re wrong? Not likely! The simplest solution would be to calculate the expected amount of dilation and then claim to have built that into the satellites.

Problem solved! The theory of relativity is not only preserved, it’s also exalted to a stage where the average Joe with a GPS receiver can vouch for relativity on a daily basis. After all, who would even suspect that atomic clocks aboard satellites might actually be running at the same rate as clocks everywhere else?

[1] A summary of 1919 eclipse problems is here http://www.simonsingh.net/media/articles/maths-and-science/1919-eclipse-and-general-relativity/
[2] http://www.mahag.com/fremd/gerber.htm - in German, see here for English.
[3] http://en.wikipedia.org/wiki/Error_analysis_for_the_Global_Positioning_System
[4] http://www.phys.unsw.edu.au/einsteinlight/jw/2006AJP.pdf
[5] http://www.phys.lsu.edu/mog/mog9/node9.html and http://www.leapsecond.com/history/Ashby-Relativity.htm and http://www.leapsecond.com/history/1978-PTTI-v9-NTS-2.pdf
[6] 442.5x10^-12 x 86400 x 10⁹ = 38232