General Relativity – part 2
We now come to the most interesting
and probably the least understood aspect of General Relativity
(GR). And that is GR’s explanation of how gravity works and
how it determines the motion of orbiting bodies.
GR is often described in terms of space bending or space
curvature. The idea being that a massive body curves the
space around it and this affects the motion of other bodies nearby,
including light. In reading the literature, one often finds
expressions such as “orbiting bodies travel in straight lines though
curved space” or “light moves along the shortest path between two
points, which will be a curve in the presence of mass.”
A popular explanation for how this works is the rubber sheet
analogy. This involves a bowling ball making a depression on
a trampoline and a marble either rolling around inside the depression
or rolling directly into it. Here the bowling ball represents
a planet, the marble a satellite, and the rubber sheet is space being
bent through an additional dimension.
These explanations can be confusing. If space was curved and
orbiting planets were following a straight path through curved space
then we would expect the curvature to be the same for all objects
regardless of their speed. In other words, an object should
follow the same orbit path irrespective of whether it was going fast or
slow. But we know that doesn’t happen.
In the case of the stretched rubber sheet, a frequent objection is that
that it requires gravity to make it work in the first place.
Without gravity there would be no ‘down’ and the marble would have no
reason to move at all. In other words the analogy is using
gravity to explain gravity. Another problem is that the
marble would create its own depression which means it would be unaware
of the bowling ball’s depression and thus wouldn’t roll into it.
Such confusion is understandable and comes from the way GR theory is
being expressed.
Well here’s some surprising news: General
Relativity has nothing to do
with space curvature. Not space
bending. Not time
bending. Not even ‘space-time’ bending. Under GR,
the distance between two points remains the same regardless of whether
gravity is present or not. What GR does have
everything to do
with is time dilation.
Here’s how it works. Under GR an orbiting body moves
according to the principle:
A body moves along
the path that makes time dilation a minimum.
That’s it! So what does this mean? Let’s take a
simple example.
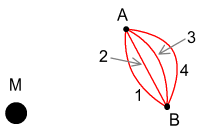 In the diagram above we have a large
mass M and
a small body moving
past it. The large mass could be the Sun or a
planet. And the small body could be a moon or grain of sand
for example. We’ll say the small body wants to get from A to
B and
needs to do so in a fixed amount of time. There are any
number of paths it could take and any number of variable speed changes
it could make along the way.
According to GR it needs to get there with the least amount of time
dilation. Now recall from the previous
chapter and the chapter on the Lorentz
transform that time dilation increases the faster we go and
increases the closer to a mass we get (i.e. it increases in higher
gravity). We want to reduce both of these. In summary:
Slow = good. Fast = bad. Low gravity
= good. High gravity = bad.
In other words we need to get from A
to B as
slowly as possible but
also while being as far away from M
as possible.
In the above diagram four sample paths are shown. The
simplest is path 2 – the straight line. This will satisfy the
condition of making the journey as slow as possible.
Unfortunately path 2 also means that most of that time is spent nearby
M, in
high gravity, and that’s undesirable. So we’ll try path
4. This one takes the object far away from M, reducing
gravitational time dilation. Trouble is, path 4 also requires
moving at high speed because the path is long and this increases
movement-based time dilation. As for path 1, that increases
dilation of both types. So it is definitely ruled
out. The correct path turns out to be 3, giving the right
balance between the two types of dilation and giving the minimum
possible amount of time dilation over all.
The best path will depend on the total time allotted in moving from A
to B.
With less time available, a straighter path is best
because it reduces average velocity. If a large amount of
time is allotted, we will instead choose a path more like 4.
All of this seems to be in agreement with the classical prediction of
gravity for orbital motion. And it turns out that the ideal
path chosen will in fact be the same as the one predicted by
Newton’s laws, with some minor differences to be discussed later.
The Schwarzschild
Metric
General Relativity usually involves
lots of complicated tensor calculus and confusing symbols.
Because of this it is best to avoid delving into its specifics until a
proper understanding can be gained at a conceptual level.
Basically however, GR is built around something called Einstein’s field
equations
and these fully describe the effects of gravity and orbital
motion. The solution to the equations involves solving
multiple differential equations simultaneously and is very difficult
except in simple situations. The earliest and best known of
these is Karl Schwarzschild’s solution for a point mass.
The ‘Schwarzschild Universe’ (to give it a name) consists of a single
point mass and no mass elsewhere. Although there may be
massless
particles nearby. For the sake of understanding we
can say
this universe contains a special clock that measures ‘universal
time’. This clock is motionless, with respect to the
point-mass, and located in a special ‘gravity-free’ zone.
This clock therefore runs faster than all other clocks elsewhere
because other clocks will be experiencing gravity which will slow them
down. And they might also be moving which will slow them
further.
We will also say there is massless spacecraft that moves about near the
point-mass. This spacecraft carries its own on-board clock
which will run slower than the universal clock.
Let the point-mass have a mass of M,
the universal clock run in
increments of dt,
and the spacecraft’s clock run in increments of
ds.
There is a formula that describes exactly how ds relates
to dt
called the Schwarzschild Metric [1].
It is:
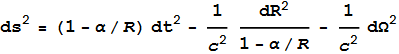 ---- (1) ---- (1)
Where (alpha) α = 2GM/c2,
R is a
function of distance to the point-mass
(see below), dR
is an increment of R
(a movement away from the
point-mass), and dΩ
is an increment in distance tangential to the
radial direction (a sideways movement) [2].
R is
described by this formula R
= (r3+α3)1/3.
Where r is
the distance to M.
For small values of α
(which is
normally the case) R
≈ r.
For very large values of M
and
small r
however, we can’t use that approximation. This
becomes important for the black-hole situation because it turns out
that 1-α/R can never become
zero without r
becoming zero. Hence
black-hole singularities cannot occur under the proper description of
GR [4].
Let’s now look at what equation (1) is saying. We’ll start by
dividing both sides by dt2,
and noting that dr/dt represents radial
velocity and dΩ/dt represents
tangential velocity. We
will also replace R
with r as a
good approximation. Taking
the square root of both sides then gives
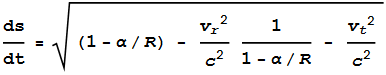 ---- (2) ---- (2)
Where vr
is radial velocity
(velocity directly away from M)
and vt
is
tangential velocity (velocity running sideways to M). Using
the relation that
1/(1-b) = 1 + b + b2 + b3 + … ≈ 1+b
(for small b)
and setting b=α/R, we can closely
approximate (2) to
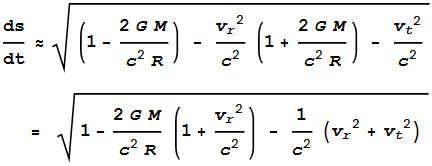 ---- (3) ---- (3)
In most cases vr<<c
and we can ignore the vr2/c2
term. Although this term will have importance in special
cases as will be discussed later. For now though, we’ll
assume vr/c=0. We
can also substitute the simple Pythagorean
sum of tangential velocity addition, that is vr2+vt2=v2
where v is
the net velocity. This makes equation (3)
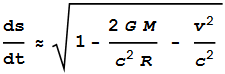 ---- (4) ---- (4)
The above should now start looking
familiar. Notice that when
we set M=0
(a zero gravity environment) we get
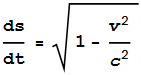 ---- (5) ---- (5)
This becomes the Lorentz
Transform! It tells us how much
slower ds
runs behind dt
when the spaceship containing clock ds
is
moving with velocity v.
Actually the Lorentz Transform is
expressed as the reciprocal of this because it describes dt/ds.
Next we again take equation (4) but and this time set v to
zero. We get
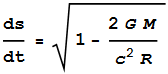 ---- (6) ---- (6)
And this is the equation for
gravitational time dilation as shown in the previous
chapter.
So what the Schwarzschild Metric tells us is the amount of time
dilation that will be experienced by a massless body in the proximity
of a point-mass based on a combination of the point-mass’s gravity and
the particle’s motion.
What is velocity
relative to?
We’ll pause here for a closer look
at the situation. In earlier chapters we looked at Special
Relativity (SR) and noted one of its main problems is we don’t know
what velocity should be measured against. Velocity is
considered a relative quantity under both SR and classical
mechanics. Therefore in order to calculate velocity-based
time dilation it is necessary to know what velocity is relative
to. In the case of SR it is ambiguous.
But this point-mass scenario would seem to solve that. Here,
all velocities are measured relative to that mass. Now look
again at equation (5). There we eliminated the mass by
setting M=0
and got the Lorentz transform. The mass is gone
but we are still measuring velocities relative to it! How can
that be? Surely the velocity term no longer has any meaning.
It gets more interesting. Instead of making M equal to zero
we’ll slowly decrease its value until it becomes insignificantly small,
like a microgram. And we’ll say the distance to our massless
spacecraft is the Earth-Sun distance. Despite M being so
small and having so little gravity, we still fully base our velocities
on it. This doesn’t seem right. Alternatively we
keep M the
same and increase the radial distance of our orbiting body
to something extreme like a billion light years. At this
distance M’s
gravity is so low it could never be detected and the
point-mass may as well not exist. Yet despite this, we again
use that mass to measure velocities against.
Something is amiss here. No one should seriously suggest that
a mass so small or far away could influence time dilation calculations
by any measurable extent. If GR were to be more credible it
should include a function in front of the v2/c2
term that decreases
with lower mass and greater distance. This appears to be a
limitation in the GR theory that either goes unnoticed or is
conveniently overlooked.
Where's the
acceleration?
Another oddity of the Schwarzschild
Metric is that it doesn’t mention acceleration.
Recall that when deriving the time dilation aspects of gravity,
the first
step was to determine how much dilation would result from
acceleration. Once having a suitable formula for
acceleration, we then substituted acceleration for gravity and arrived
at an equivalent formula for gravity. So we have our
time
dilation formula for gravity. But having achieved this, for
some reason we now regard the acceleration formula as
unimportant.
When planets orbit the Sun they are constantly changing direction and
hence constantly experiencing acceleration. If acceleration has
an effect on time dilation we should therefore expect the Schwarzschild
Metric to somehow account for it by including terms for
acceleration. If the Metric did include acceleration terms they
would
appear as d2R and d2Ω [3].
But such terms are clearly absent. Why so?
One
problem of including acceleration terms is that the predictions for
orbital motion will be wrong. This however, is not a valid
reason for their exclusion. Rather, it indicates that either
the Metric is wrong or that the fundamentals of GR are wrong.
Light-bending and
Perihelion advances
We’ll now turn to a more
interesting
aspect of GR. This is where GR makes predictions different
from what classical mechanics would make. The first of these
is light-bending.
If we were to assume that Newtonian gravity affects light the way it
affects regular matter, we could calculate the degree of bending a
light-ray would experience as it passed by a massive object such as
the Sun. GR also predicts light will be bent but it predicts
double the amount Newtonian gravity would. Why is this?
Go back to equation (3). If we take this and include the net
velocity relationship, vr2+vt2=v2
(as was included in equation (4)),
we get
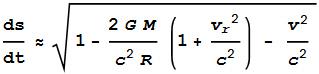 ---- (7) ---- (7)
Notice the vr2/c2
term.
In equation (4) we removed this
because it was small for orbiting planets and satellites. But
for light itself it will be large. As a ray of light skims
past the Sun, vr2
will be very close to c2.
That means the
term inside the parentheses becomes almost equal to 2. And we
get
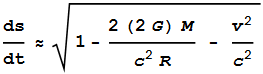 ---- (8) ---- (8)
Without going through the
complicated math, what we have effectively
done is double the value of the gravitational constant. This
equates to doubling the ‘force’ on the light ray and we end up with
twice the bending. There’s obviously more to it than that but
that’s the basic idea.
The next prediction GR makes that is at odds with Newtonian gravity has
to do with elliptical orbits gradually changing their
orientation. This is known as ‘advancement of perihelia’ and
becomes noticeable for planets with stronger elliptical orbits, such as
Mercury. What makes this happen?
In an elliptical orbit a planet spends some of its time moving toward
and away from the Sun. That means the radial
velocity vr
is
non-zero. We’ll take equation (7) and rewrite it in terms of vt
and vr.
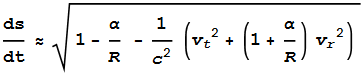 ---- (9) ---- (9)
We want to make (9) a maximum, i.e.
make time dilation a
minimum. We already know this requires reducing overall
velocity (velocity = bad). What (9) tells us is that radial
velocity has a slightly greater impact on dilation than tangential
velocity (radial velocity = slightly badder).
Another thing (9) tells us is that the impact of radial velocity
becomes greater with smaller values of r (closer to the
Sun) and its
impact is reduced as the planet moves farther away.
Therefore, in order to reduce time dilation, the planet will need to
adjust its orbit to accommodate this. This can be done by
reducing its outward velocity when it is close to the Sun, then
increasing it as it moves farther away. The overall result is
this:
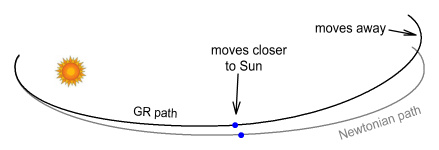
The grey line shows what Newtonian
gravity predicts. The
black line is what GR predicts. As the planet begins moving
away it slows down, making it closer to the Sun, and then speeds up as
it gets farther away. Here the blue dot indicates a point
that has moved closer. The result is the far-point of the
ellipse (the aphelion) is shifted along slightly. A similar
thing happens on the return trip in which the near point of the ellipse
(the perihelion) advances slightly with each orbit.
Again there’s obviously more to it than that and the math is very
complicated. But that’s the basic idea.
Another Equivalence
problem
The
fact that GR predicts a different amount of bending for light presents
another problem for the Strong Equivalence Principle. This
principle claims that if you were sealed inside an elevator you
wouldn’t know if it were sitting motionless on Earth or accelerating
through outer space at a rate of 9.8 m/s2.
But if the
above GR prediction is true then it appears there’s a way after
all. Simply shine a laser across the elevator. If
the light
bends in a manner predicted by Newton, you’re in space. If it
bends with double that amount, you’re on Earth. This means
that,
according to GR theory, gravity is not equivalent to acceleration after
all.
Vertical motion
Most of the discussion so far has
been about orbital motion. That is, bodies moving around a
point mass at periodic intervals. But GR can be applied to
any type of motion such as vertically falling or rising objects.
Suppose you threw a stone directly upward. Experience tells
us that the stone will begin its journey at full speed, gradually
slowing to a stop, then falling again. Classical mechanics
tells us that its motion will be a parabola when plotted against time.
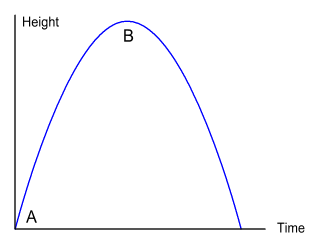
It’s interesting to note that GR
predicts the same thing. If
we label your hand as point A,
the top of the parabola as point B,
and
specify the time it takes to get there, GR also predicts the stone will
slow as it moves upward. Why it that?
Let’s say instead of a stone you were shooting a high-speed projectile
several hundred km into space and there was no atmosphere to slow
it. GR aims to minimise the extent of time
dilation. When the projectile is farther from Earth,
gravity is lower, and hence time dilation is lower. So GR
‘decides’ to have the projectile spend most of its time farther
away. To do this the initial velocity is set high and the
ending velocity is low.
Without going through the maths it turns out that the ideal solution
for least amount of dilation is also the classical mechanics prediction
(ignoring the microscopic GR adjustments described earlier).
And for a falling object the reverse will be true.
The interesting question here is how is GR able to distinguish between
minor differences in gravity? For an object rising hundreds
of km above Earth, this is easy because gravity drops
measurably. But what about throwing a stone upward by a few
inches – how can GR detect any difference in gravity over that small
distance? If there is no difference in gravity over a small
range then presumably GR would keep velocity constant.
Of course there must be some
difference in gravity over any vertical
distance. And presumably GR is somehow detecting it and
taking it into account. Fortunately there is a way to
determine whether that is the case. Above the Earth’s
surface, gravity decreases with altitude. But below the
surface the opposite happens. That is, gravity decreases with
depth, becoming zero at Earth’s centre.
So the test is this: Stand inside a mine shaft and throw a
stone upward. As the stone moves upward it experiences an
increased downward pull. This is the opposite of what you get
above ground. If GR were based on subtle gravitational
differences then we would expect it to require the stone to begin
slowly and increase speed toward the top. But we don’t see
this. Instead the stone moves in much the same way as it does
above ground, i.e. in a parabola. This would suggest that GR
is not responsible for the stone’s motion after all.
[5]
The stationary particle
We’ll now look at a situation that
GR genuinely has problems with. Suppose you observed a
particle to be
situated some distance away from Earth. Your observation was
made using high-speed film and the photograph gave no clue about which
direction the particle was moving because there was no blur.
Several hours later you took another photo and found the particle at
the same location. Based on your understanding of gravity you
would know that it is impossible for the particle to have been sitting
there the whole time. So you would conclude that the particle
must have either orbited the Earth and returned to the same point, or
was earlier moving upward and had then fallen down to that same point.
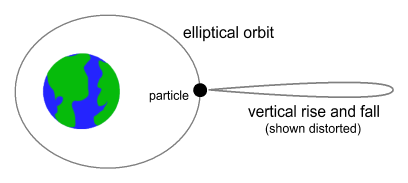
GR would also draw the same
conclusion and say the particle must have
taken one of those two paths. Problem is you wouldn’t know
which. In both cases, classical and GR, you’d be lacking
information.
If you want to know how a particle orbits using classical mechanics all
you require are its ‘initial conditions’. This information
consists of the particle’s starting position and velocity.
With this information the force on the particle can be calculated and
incremental steps in its position can be mapped into a complete
orbit.
With GR it’s a bit different. To know a particle’s path we
need both a start and end location and the time taken to get
there. Knowing the start point is easy because that’s what we
begin with. But the end-point and time taken... how can these
be known in advance?
Under GR a particle’s initial condition consists of position
only. We don’t care about velocity. But let say we
knew both position and velocity. Using that position and
velocity, and ignoring the acceleration predictions of Newtonian
gravity, we can calculate the first step in its journey for a small
increment of time. That gives us two points in the
orbit. From then onward we can use GR to calculate additional
steps. Each additional step will be determined such that it,
and the two steps before it, give the minimum amount of time dilation
possible. It’s a complicated process but certainly
doable. In this way a GR-based orbit can be determined based
on initial conditions only.
But let’s say the particle was initially at rest. In this
case we won’t know what the second point in the orbit is because zero
initial velocity means no initial movement. Because of this
GR can’t tell us what any of the following points will be.
This isn’t a problem under classical mechanics because Newtonian
gravity predicts a downward acceleration and we can determine the
second point in the orbit will be underneath the first.
Presumably then we could use both velocity and Newtonian gravity to
calculate this second point for GR also. However this would
be cheating
because we are not supposed to use Newtonian gravity theory: GR is
supposed to fully determine the motion based on time dilation aspects
alone.
This is not to say that GR would permit the particle to stay
still. Certainly not. GR would require it to move
in order to minimise time dilation. Problem is, GR cannot
tell us how a stationary particle should begin moving. This
is a definite failing in GR theory.
But let’s get back to the case where a particle did have some initial
motion. In that case we used its initial velocity to
determine the second point in the orbit. Here again though,
we are stepping outside of GR in order to compute the continuation of
an orbit. Strictly speaking we should not be using any part
of classical mechanics because GR is supposed to fully account for the
path on its own. In fact, the Schwarzschild Metric is often
used to derive classical laws such as the conservation of energy and
angular momentum. This derivation would have no validity if
it required classical laws as part of the input.
Questioning the motion
This leads us to some important
questions about what GR is describing. Under classical
mechanics a body can only respond to the forces that are acting upon it
at the time. It can’t base its motion on something that it
will encounter later on. Yet GR seems to describe a body
doing exactly that. Namely that a body determines a path to a
destination that it doesn’t yet know of, based on
conditions it
has not yet encountered. How is this possible?
Given that it’s not possible to reverse the roles of cause and effect,
GR cannot be acting as a predictor for what is about to
happen. Rather, it acts as a verifier for what has already
occurred. What GR says is: show me an orbit path segment and
I’ll tell you whether it’s valid or not.
Based on this, it is safe to say that GR is not governing the motion of
orbiting bodies. Rather, a separate process must be
responsible for determining how bodies move in the presence of a
gravitational field. We know that Newtonian gravity can
accurately account for the majority of such motion. But
Newtonian gravity has limitations, such as not explaining
perihelion-advancement.
Thus, rather than replace Newton’s gravity equation with GR, it would
seem wiser to retain and make adjustments to it. In order
that the cause and effect principle is not violated these adjustments
should describe forces that are solely determined by the information
that is able to be ‘felt’ by the orbiting body at the time.
Conclusions
The acceleration time dilation
aspects of General Relativity (GR) are internally self-contradictory
and thus could not be true.
The
Strong Equivalence Principle between gravity and acceleration fails
because the time-dilation formula for gravity includes a body’s radius
in addition to its field strength. It also fails because GR
predicts a different degrees of bending for light in a gravitational
field versus an equivalent accelerating reference frame.
The Weak Equivalence Principle contains no information that is not
already contained in the Newtonian description of gravity.
GR can accurately describe the path of a free-moving body in the
presence
of a gravitational field and can do so with greater accuracy than
Newton’s gravity equation.
GR seems illogical in determining how relative velocity is measured;
especially when small masses or large distances are involved.
GR cannot predict an orbit-path in advance. It can only
verify whether a potential orbit-path is valid.
GR cannot determine how a motionless body should accelerate in the
presence of a gravitational field.
[1]
Schwarzschild’s original paper in
English http://arxiv.org/PS_cache/physics/pdf/9905/9905030v1.pdf
[2]
dΩ is
normally expressed in terms of spherical coordinates R, ϑ
and φ.
[3] After dividing both
sides of (1) by dt2 these will become
the familiar acceleration terms d2R/dt2 and d2Ω/dt2.
[4] See this site for a
detailed discussion of why GR forbids black-hole singularities http://sjcrothers.plasmaresources.com
[5] Due to Earth’s the high-density core and
low-density crust, gravity below the surface initially increases with
depth. In actuality you’d need to go down several thousand
km before the gravity dropped below its surface strength. But if
you did throw a stone upward from such a depth, there’s no reason
to believe it would speed up as it moved away from your hand and into
stronger gravity.
|

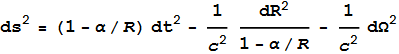 ---- (1)
---- (1)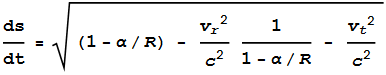 ---- (2)
---- (2)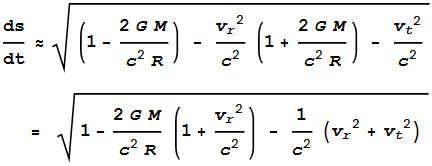 ---- (3)
---- (3)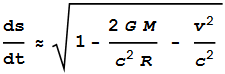 ---- (4)
---- (4)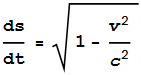 ---- (5)
---- (5)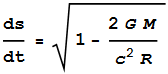 ---- (6)
---- (6)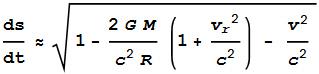 ---- (7)
---- (7)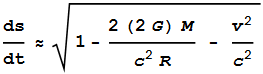 ---- (8)
---- (8)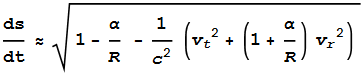 ---- (9)
---- (9)

