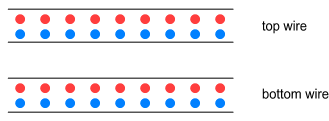
Magnetic Test of Length Contraction

A derivation often cited as proof for Length Contraction (LC) involves an explanation of magnetism in terms of Special Relativity [1]. The derivation shows how, due to LC, moving charged particles will appear closer together. This makes their charge density appear greater to a motionless particle and thus produces a higher attraction on a motionless particle of opposite charge, leading to what we observe as magnetic force.

Here’s how it works. Below are two lengths of electrical wire set in parallel:

The wires contain equal amounts of positive and negative charge so they exert no net force on each other.

Next we start an identical current flowing in both wires. The wires have the same cross-section so electrons in both wires move to the right with equal velocity.

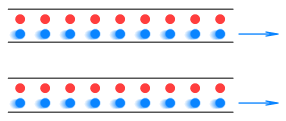
Here’s where LC comes into play. Because the electrons are moving, they appear to compress along their length and become closer together. Here’s what the protons see:

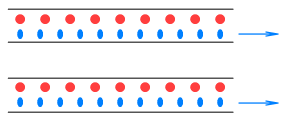
The electrons on the other hand see themselves as still (due to identical velocities) and the protons as moving to the left. Here’s what the electrons see:

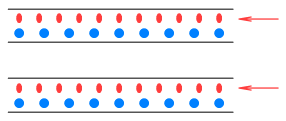
LC brings the charges closer together, making the density of opposite charges appear higher. As a result the electrons in one wire experience increased attraction to the protons in the other wire and vice versa, leading to the wires being attracted to each other.

A detailed analysis shows that the amount of attraction between wires corresponds exactly to the magnetism that would be expected for given currents and distances [2]. This supposedly explains how magnetism works and proves LC is real.

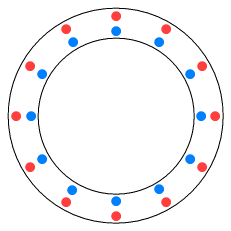
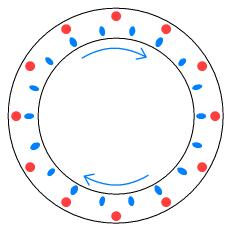
Problems

The LC works well as an explanation for the magnetic force between straight wires. Let’s now look at another situation: coils. Below we see a piece of wire curved into a loop. We wish to know the influence of magnetism in the middle of the loop. Initially there is no current in the wire. From the view-point of a charge at the middle of the loop it looks like this:

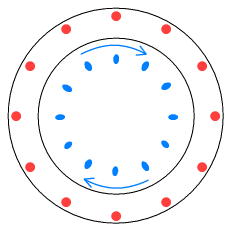
Now we turn on the current and the electrons flow clockwise. According to the relativistic proof of magnetism, from the viewpoint of a stationary observer, the wire should look like this:

See the problem? In order to increase charge density it was necessary to increase the number of electrons in the wire. But this is impossible because the total number of electrons cannot change. Special Relativity does not provide any mechanism for creating new charges.

Since the magnetic field in the middle of the loop is not zero, this shows LC cannot account for magnetism in this case.

The only way to make the LC proof work here is to relocate the moving electrons inward, like this:

This would increase charge density without adding more electrons. But it would also contradict the straight wire situation where the moving electrons relocated themselves at some point along their path of travel, rather than at a point perpendicular to their motion.

Conclusion

Magnetism cannot be cited as a validation for relativistic length contraction because it only predicts the correct result in some situations and not others.

Another issue is the question of which direction the contraction should be occurring in. Normally LC is described in terms of an object moving directly toward or away from an observer, with the length contracting along that same direction. But here the movement is at right angles because that’s what magnetic force requires. Therefore we ought to wonder whether LC is being properly applied to this situation.

A final point to be made is that the LC cannot be used as an outright proof of magnetism because other models can be constructed to also account for it. An alternative explanation for magnetism, which does not require relativity, is given in a following chapter.

[1] Originally shown by Edward Purcell in Electricity and Magnetism
[2] E.g. http://galileo.phys.virginia.edu/classes/252/rel_el_mag.html