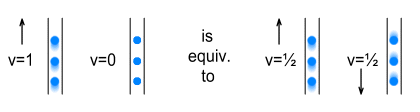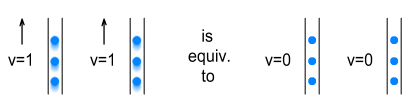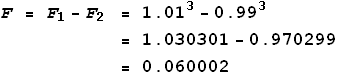Magnetism Explained

Magnetism is a phenomenon by which materials and electrical currents exert an attractive or repulsive force on other materials and electrical currents. It’s a force that appears to associate with moving electrical charges, such as an electron circling a nucleus, moving along a wire or through a vacuum tube.

Magnetism is often described within the term ‘electromagnetism’ implying that it is somehow linked with electrical forces. How does magnetism work and what is its relation to the electric force? In this chapter I will attempt to explain the relationship.

First let’s look at some simple electrical experiments involving the magnetic force between current carrying wires:

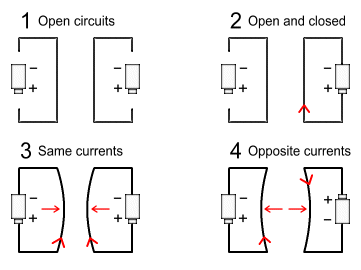
In the above diagram:
1. Both circuits are open and no current flows. There is no force between the wires.
2. Current flows in one wire but not the other. There is no force between the wires.
3. Current flows in a similar direction in both wires. There is an attractive force between the wires.
4. Current flows in opposite directions in the wires. There is a repulsive force between the wires.

How do we explain this? Experiment 1 appears straight forward. Both wires are electrostatically neutral in that they contain an equal number of positive and negative charges. Therefore we don’t expect any net force to exist between them. Likewise with experiment 2. But what about experiments 3 and 4? Those wires are also neutral so there shouldn’t be any force between them.

The experiments indicate that magnetic force occurs only when moving electrical charges interact with other moving electrical charges. In other words, unless current is flowing in both wires, nothing happens. This is undoubtedly true but it does raise some important questions:

1. In experiment 2, on what grounds can we say that current is not flowing in the open circuit? From the view-point of the batteries, certainly there is no net electron motion occurring. But from the view-point of the electrons in the the closed circuit wire, the electrons in the other wire are moving. In other words, there exists a velocity difference between the electrons in both wires and therefore, we would expect magnetism to occur [1]. This diagram shows the equivalence:

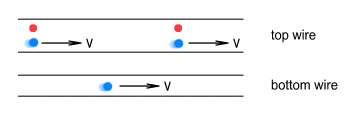
2. In experiment 3, on what grounds can we say that current is flowing in either wire? From the view-point of the batteries, electron motion is certainly occurring. But from the view-point of electrons in each wire, the electrons in the other wire are motionless. In other words, there is no velocity difference between the electrons and therefore, we would not expect magnetism to occur. This diagram shows the equivalence:

Clearly there is more to magnetism than meets the eye. Below I will attempt to explain just how it might occur in terms of electrical forces.

Using Coulomb’s Law to predict magnetism

In an earlier chapter on relativistic mass, I proposed that electrical forces between charged particles depend not only on their charge and distance, but also velocity. I then proposed a modification to Coulomb’s law, called Velocity Dependent Coulombs Law (VDCL) that incorporated velocity into the equation. Basically the force between charged particles is proportional to the cube of the difference between their velocity and the field velocity, i.e.

$F \propto (c-v)^3$

Where F is force, v is velocity and c is the field speed that is equal to light speed. Let’s see how this applies to moving electrical currents.

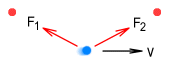
In the diagram below an electron is moving past two protons. The electron is inside one wire and the protons are inside another parallel wire.

The electron experiences an attractive force from each of the protons. Let the force from the first proton be F₁ and from the second be F₂. If the electron is travelling at velocity v, what will the forces be? For simplicity we will replace the proportional sign with an equal sign:

$F_1 = (c+v)^3\text{ };\text{ }F_2 = (c-v)^3$

In this case the velocity term is positive for F₁ and negative for F₂ because the directions are different. To calculate the net force we take the difference between these forces, ignoring vector (directional) calculations for now. For example, suppose that v is 1% of light speed (0.01c), we can calculate the net force as:

F = F_1-F_2 = 1.01^3-0.99^3 = 1.030301-0.970299 = 0.060002

Notice that the difference between F₁ and F₂ is larger than the difference between their velocities, which is 0.02. That is because the cube (the 3^rd power) increases the larger number more quickly than the smaller number. This is important because it means that the net force F is now greater than it would have been if the electron was not moving. In other words it appears that the force between the particles has increased due to their movement. Could this increase in the electrical force be related to magnetism?

Currents in the same direction

Let’s look more closely at the situation with force between currents running in the same direction. The above example was a simplification because it did not take into account the various forces from both the positive and negative charges in the other wire. Consider the below diagram that shows a pair of parallel wires carrying identical currents:

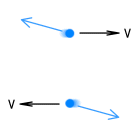
Both wires contain equal numbers of protons and electrons. As expected, the protons stand still while the electrons freely move in the same direction. For simplicity I have shown only a single electron in the bottom wire. The below diagram shows the various forces on this electron:

The blue lines show forces from the above electrons. These forces will be exactly symmetrical because the electrons are motionless relative to one another. The red lines show forces between the protons and the bottom electron. Notice that the backward force is very strong and the forward force is quite weak due to the VDCL discussed above. Putting all these force vectors together, the net force will look like this:

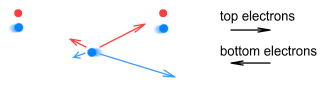
The net force on the bottom electron is upward and to the left. If we were to determine the net force on a top electron we would find that it is downward and to the left:

The result of this is that the two wires will force themselves together, just as we observe in experiment 3.

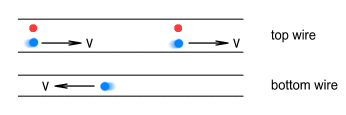
But what about that backward (to the left) force: won’t that cause the wires to also recoil backward? Actually it won’t because the force is applied to the electrons, not the wires. The electrons are ‘free floating’ and any force applied to them along the direction of the wire can only cause them to move along the wire. In this case the force will create a resistance to their forward movement. But the only force each wire feels is an attractive force at right angles towards the other wire.

Currents in the opposite direction

Now let’s look at what happens when currents run in an opposite direction. Consider the below diagram that shows a pair of parallel wires carrying identical but opposite currents:

This is more complex than when currents move in the same direction because the electron in the bottom wire is moving in opposite directions to both the protons and the electrons in the top wire. The important point here is that the speed difference between electrons is twice as great as that between the protons and the electron. As a result the net force between electrons will much greater than between the protons and the electron. The below diagram shows the various forces on the bottom electron:

Note the following:
. The force from the protons is the same as in the previous example, but in the opposite direction.
. The backward force from the top-left electron is very strong because of the large speed difference.
. The forward force from the top-right electron is very weak because of the small speed difference.

Putting all these force vectors together, the net force will look like this:

The net force on the bottom electron is downward and to the right. If we were to determine the net force on a top electron we would find that it is upward and to the left:

The result of this is that the two wires will force themselves apart, just as we observe in experiment 4. Like the previous example, the electrons also experience a backward force against their direction of travel. Again, this will not cause the wires to recoil; it will only create a resistance to the electrons’ movement through the wires. In this case the backward force is greater and may be felt as an ‘inductive resistance’. But the only force each wire feels is a repulsive force directed at right angles away from the other wire.

Conclusion

Using the VDCL we can see how electrically charged particles may interact in a way that produces forces in directions precisely corresponding to the forces of magnetism. Once we understand the velocity dependent nature of electric forces, we can predict how magnetic effects follow from it. Additionally, related effects such as magnetic induction can be predicted.

The pioneers who originally produced the magnetic force equations (such as Maxwell, Gauss, Faraday and Ampere) recognised a direct relationship between magnetic force and electrical current, but were unable to describe a mechanism by which it might operate. Modern theory does not provide much explanation for magnetism either, except to say that it has some relation to relativity theory and electron spin. The above examples combined with a more detailed calculation in the following chapter indicate that the VDCL is quite likely the correct explanation of magnetism.

-----------------
[1] Experiment 2 can influence a fixed magnet such as a compass needle, but that is because a magnet contains flowing charges, making it akin to experiments 3 and 4. For the purposes of this discussion we are only interested in the interactions between the two wires.