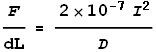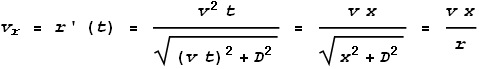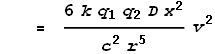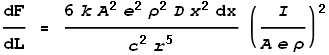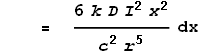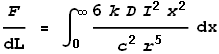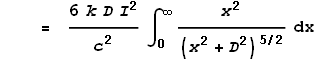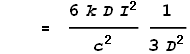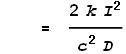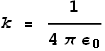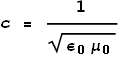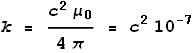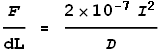Magnetism – Proof of Concept

In the previous section we looked at how the phenomenon of magnetism might be understood in terms of an increase in the electrical forces due to movement of charged particles through each other’s fields. The diagrams showing forces between current carrying wires gave a good idea of how something resembling a magnetic force could arise from a velocity-dependent electric force.

Diagrams are useful for showing how an idea works in principle. But to really be sure one needs to examine the setup in detail. In this section I will go more deeply into the calculations to show that the magnetic forces predicted by the Velocity Dependent Coulombs Law (VDCL) are in fact a perfect match for the conventional magnetic force equations.

There’s a lot of maths here (!) so you may want to skip to the conclusion.

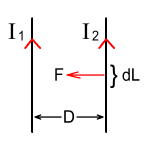
Force between wires

To test the theory out, we’ll look at the magnetic force between parallel wires. Suppose we have two parallel wires as shown below:

The wires carry currents of I₁ and I₂ respectively and are separated by a distance D. What will be the magnetic force F experienced by each wire per unit length dL be? Magnetic force equations tell us that:

$\frac{F}{\text{dL}}=\frac{ \mu _0 I_1 I_2}{2 \pi D}\text{ where }\mu _0=4 \pi 10^{-7}$

To simplify the calculations, let’s say the current in both wires is I. The force per unit length will be:

$\frac{F}{\text{dL}}=\frac{ 2\times 10^{-7} I^2}{D}$

And this is the result we are aiming for.

Using the VDCL

Now let’s see what we predict for magnetic force using the VDCL. First we note that that each wire holds equal numbers of protons and electrons, giving the wires a neutral charge. Most of those electrons are fixed while others are ‘free floating’ and able to carry a current. We can eliminate the fixed electrons and a corresponding number of protons from our consideration because they have no net effect. What remains then is only the floating (current carrying) electrons and an equal number of unmovable protons.

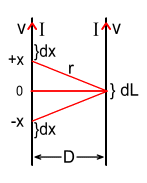
Consider the two wires again as shown below.

Let’s look at the force produced in a small section of the right-hand wire of length dL, by two small sections of the left wire of length dx located at distances of +x and –x from the centre. The force on the wire segment dL is made up of the repulsive force from the electrons and the attractive force from the protons. Assume each wire has the same cross sectional area of A and the velocity of the electrons in each wire is v. Also let the charge located within a dx segment be q₁, and the charge located within the dL segment be q₂.

The electrons in both wires are moving with identical velocity because the current and cross sectional area are the same. This means that the electrons are standing still relative to one another. So the horizontal force F_e from the electrons can be calculated using the standard Coulombs law:

$F_e = 2\times \frac{-k q_1 q_2}{r^2} \frac{D}{r}\ = \frac{-2 k q_1 q_2 D}{r^3}$

Where r is the distance from dL to dx and is given by:

$r = \sqrt{x^2+D^2}$

Now to calculate the force from the protons. To do this we must consider the velocity of the protons relative to the electrons. The velocity v_r at point x relative to dL can be determined from the rate of change of the distance r.

$r(t) = \sqrt{(v t)^2+D^2}$

$v_r = r'(t) = \frac{v^2 t}{\sqrt{(v t)^2+D^2}} = \frac{v x}{\sqrt{x^2+D^2}} = \frac{v x}{r}$

Using this velocity function in the VDCL, the (stronger) force from the protons at -x can be given by:

$F_{\text{p1}} = \frac{k q_1 q_2 D}{r^3}\left(1+\frac{v x}{r c}\right)^3$

The (weaker) force from the protons at +x can be given by:

$F_{\text{p2}} = \frac{k q_1 q_2 D}{r^3}\left(1-\frac{v x}{r c}\right)^3$

The total force can be calculated by adding forces from both protons and electrons at both positions (+x and -x). Doing this we get:

$\text{dF} = F_{\text{p1}}+F_{\text{p2}}+F_e$

$\text{ }=\frac{k q_1 q_2 D}{r^3}\left(\left(1+\frac{v x}{r c}\right)^3+\left(1-\frac{v x}{r c}\right)^3-2\right)$

$\text{ }=\frac{k q_1 q_2 D}{r^3}6\left(\frac{v x}{r c}\right)^2$

$\text{ }=\frac{6 k q_1 q_2 D x^2}{c^2 r^5}v^2$

This shows the force in terms of the velocity v. But we want it in terms of the current I. To do this we use the electron density conversion formula:

$v = \frac{I}{A e \rho }$

Where ρ is the electron density per cubic volume, A is the cross sectional area of the wire and e is an electron’s charge. We also need to express the charges q₁ and q₂ in similar terms:

$q_1 = A e \rho \text{dx}\text{ ; }q_2 = A e \rho \text{dL}$

Substituting these values of velocity and charge into the force expression we get:

$\frac{\text{dF}}{\text{dL}} = \frac{6 k A^2 e^2 \rho ^2 D x^2 \text{dx}}{c^2 r^5}\left(\frac{I}{A e \rho }\right)^2$

$\text{ }= \frac{6 k D I^2 x^2}{c^2 r^5}\text{dx}$

This gives the force from just the two points at dx. To determine the full force from the entire length of the left wire we must integrate the above expression over all positive values of x:

$\frac{F}{\text{dL}} = \int _0^{\infty }\frac{6 k D I^2 x^2}{c^2 r^5}\, dx$

$\text{ }=\frac{6 k D I^2}{c^2}\int _0^{\infty }\frac{x^2}{\left(x^2+D^2\right)^{5/2}}\, dx$

$\text{ }=\frac{6 k D I^2}{c^2}\frac{1}{3 D^2}$

$\text{ }=\frac{2 k I^2}{c^2 D}$

Coulombs constant k can also be expressed as:

$k = \frac{1}{4 \pi \epsilon _0}$

Maxwell’s and Ampere’s laws tell us that:

$c = \frac{1}{\sqrt{\epsilon _0 \mu _0}}$

Extracting ε₀ and substituting it into the equation for k we see that:

$k = \frac{c^2 \mu _0}{4 \pi } = c^2 10^{-7}$

Substituting this value of k into the force equation we get:

$\frac{F}{\text{dL}} = \frac{2\times 10^{-7} I^2}{D}$

This is the exact result we were after! Namely, the VDCL has computed the magnetic force equation.

Conclusion

Based on the above calculations, we can see that the VDCL can be used to determine the exact result as Maxwell’s magnetic force equations.

Does this prove that the VDCL is valid? Not necessarily, because the form of the VDCL was chosen to achieve the desired result. For example if instead of cubing the velocity, a square was used, the result would be smaller by a factor of three. This is the reason a cube was chosen over a square. Additionally, the faster-than-light calculations favour a cube over a square as previously shown.

But what we can conclude is that the VDCL has a high probability of being correct; namely: that the force between charged particles varies in proportion to the cube of the difference between their relative velocities and the speed of light.

Wait... a mistake?

The above calculation only determines the force from the protons in the Left wire upon the electrons in the Right wire. But the Right wire also has protons that will be attracted to the electrons of the Left. If this is included the total force per unit length will be twice as large. Are our results too small by a factor of 2?

As it happens the above formula is correct because it is only intended to determine the force of one wire upon the other; and this is what the definition of an ampere is based on. Actually this will be the net force between a wire and an electron beam of equal current because the electron beam has no protons and cannot pull against the wire. But the force between two wires will be double that amount.

One final point worth mentioning is that the ‘magnetic’ force between two electron beams, whose electrons are travelling at the same velocity in both beams, will be zero because there are no stationary protons to pull against. In fact there will be a net repulsion because the electrons are like-charged and motionless relative to each other.

For a detailed generic proof see:
Magnetism – Proof of Concept, part 2.