Ideas for Propellantless Propulsion
It could easily be argued that the greatest challenge facing the
promise of long-distance space travel is the aspect of
propulsion. When vehicles on Earth’s surface or within its
waters or atmosphere move about, they generally do so by pushing
against their surrounds. Cars use wheels to push against the
road, boats use propellers or paddles to push against the water, and
helicopters use rotors to push against the air.
Vehicles in space don’t have that luxury. With no surrounding
mass to push against, the only way a spacecraft can move forward is by
throwing material – usually rocket exhaust – in the opposing
direction. This all works very well, until that is, the
material to be ejected is used up. Thereafter the craft
drifts at constant velocity and at the mercy of gravity [1].
Overcoming this limitation appears to leave us only two options: either
bring along more material when starting a journey, or find a way of
ejecting the material at higher speeds. The first option is
problematic because it makes the vehicle heavier: making it harder to
launch against gravity in the first place, and harder to accelerate
once in orbit. The second option seems wiser and might be
achieved by finding more powerful chemicals or higher-energy ‘ion
thrusters’.
But for long journeys, both methods are doomed to failure.
Once the material is gone, it’s gone, and can’t be re-ejected.
What then if there were a way of producing forward motion without
pushing against external objects or ejecting propellants?
This suggestion must sound crazy, impossible in fact. Physics
laws tell us that the interaction between two objects produces equal
forces in opposite directions; such that two components of a spaceship
pushing against each other could produce no net force in any direction.
This is often phrased as “for every action there is an equal and
opposite reaction”.
This is Newton’s third law of motion and understood in terms of
conservation of momentum. It is what rockets rely on as they
push a small amount of mass (the exhaust) backward at high speed, to
move a large amount of mass (the rocket) forward at a lesser
speed. In fact it is what all forms of transport ultimately
rely on: for a car to drive forward it needs to push the Earth slowly
backward – momentum is conserved in both situations.
In an earlier article (see here),
I argued that this law is just an
approximation, albeit a very reliable one for most
situations. The reason is that the speed of light is finite,
and a change in motion of one charged particle takes a short while to
be communicated to the other. As a result there is a delayed
response and momentum can end up not being perfectly preserved.
I also suggested it may be possible to take advantage of this to
accelerate a spacecraft without ejecting a propellant. And
that providing we had enough energy to power the process, the velocity
would keep increasing essentially without limit.
This suggestion caught the attention of a few people (including a
science fiction author) who were keen to know the practical aspects of
this idea – about how it might be constructed, and whether the net
force would be enough to be usable. Here I’ll attempt to do
just that, although the method will be different from the one earlier
described.
The carousel
To understand the concept it is best to start with a simple
analogy.
There is a carousel (a circular rotating platform, also called a
merry-go-round) in a playground. Two boys stand on
it. One stands in the middle and the other on the outside
edge. They each have a supply of tennis balls that they will
throw at the other. They throw balls at the same speed and
simultaneously. We’ll also say that when they throw a ball in
a particular direction, they throw another ball in the opposite
direction and at the same speed. This is to prevent them from
accelerating when throwing balls. We’ll also say that they
throw the balls once per second and at a speed of 5m/s.
Start with situation where the carousel is not rotating. Each
boy throws a ball toward his opponent while throwing another ball
away/backward. A short while later the balls arrive at their
target and apply a force. If the carousel’s surface was
highly slippery, at the point when the balls were thrown, neither boy
would move. But when the balls hit, both boys would slide
backward. But we’ll say the surface isn’t slippery and they
wear rubber shoes. In this case the carousel floor would be
stretched slightly.
Now to start the carousel rotating. The boys throw their
projectiles and now find they both miss – although for different
reasons. The one standing in the middle of the carousel
misses because the other has moved from where he was when ball was
thrown. While the one standing on the outside misses because
his sideways speed gets added to the ball, throwing it off-target.
Shortly afterward they each realise their mistake and adjust their
aims: the one in the middle aims at future position of the “outsider”,
while the “outsider” aims slightly in the opposing direction of the
carousel’s motion.
It might seem that everything is back to normal, and that the resulting
forces of impact are equal and opposite. But that’s not the
case. When the boy in the middle threw his ball, it hit the
“outsider” at the same speed and applied the same outward
force. It also applied a force in the reverse direction of
carousel motion – however we will be ignoring this for this
exercise. Now when the “outsider” threw his ball, he needed
to do so at a backward angle, in order to negate the carousel’s
motion. As a result the speed of the ball in the direction of
the target was reduced and the ball applied less force. This
diagram explains the situation:
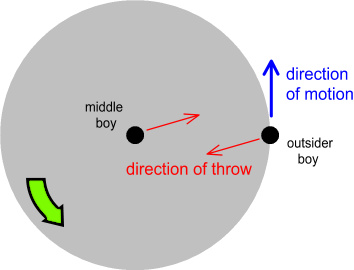
From the perspective of someone standing on the carousel, the forces
are no longer equal and opposite. Instead there is a net
force in the outward direction.
Now step this up a notch. We increase the speed of the
carousel until it is moving at the same speed as the boys throw the
balls – 5m/s. The boy in the middle can still hit the
outsider by aiming at a future position even further ahead.
But the outsider finds he can no longer hit the one in the middle –
even increasing the angle of throw to 90 degrees won’t do it.
The force is now one-sided and fully outward. If the carousel
were mounted on a slippery surface, we would expect it to launch
slightly in that direction when the ball hit the “outsider” target.
Circling charges
Alas nothing useful has been achieved here because we are propelling
the carousel by ejecting tennis balls in the opposing direction, making
them an “external propellant”. But this scenario was just an
analogy to the main point that follows.
Let’s change the situation by considering two positively-charged
spheres, such as what would found atop Van de Graaff
generators. They are connected by a joining rod.
One sits motionless while the other is made to orbit it.
As before, start with the situation where they are standing still (no
orbiting). Each sphere exerts a repulsive force of equal and
opposite magnitude on the other, and the connecting rod is stretched,
preventing them from moving apart. As a result there is no
net force and everything remains still.
Now start the orbiting process. This can be done by placing
them on a turntable with the motionless sphere in the centre.
To prevent the turntable wobbling, we’ll also place an uncharged sphere
of identical mass and distance on the opposite side of the orbiting
sphere.
Each sphere continues to push against the other but the situation is a
bit different. Referring back to the carousel example, the
boys represent positive charges and the tennis balls represent a
radiating electric field.
Just as with the boys on the carousel, the field that radiates from the
orbiting sphere needs to originate from a slight angle in order to hit
the motionless sphere. This means it will hit the motionless
sphere at a speed slightly less than c, the speed of light.
Whereas the field that comes off the motionless sphere will continue to
hit the orbiting sphere at speed c. Actually it will be
slightly greater than c, due to the forward motion of the sphere
being hit, but we’ll ignore this for now. This diagram describes
the situation:
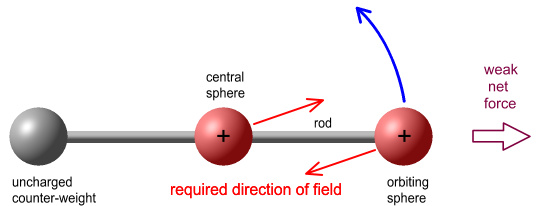
To understand the implications of this, refer back to earlier chapters
(here & here) where it argues
that electrical force is a function of impacting field speed, such that
(for like-charges) force will decrease as the field speed decreases,
much like how the tennis ball’s force decreased with impact.
If this is correct, then it would seem that there would be a net force
in the outward direction, toward the orbiting sphere. If the
turntable were sitting on a frictionless surface we would expect it to
launch in that direction.
Unfortunately this is not helpful because the force direction is
continually changing, meaning all that would happen is that the
turntable would wobble. So let’s make a couple of changes.
The first change is to replace the orbiting sphere with a charged ring
that circles the central sphere (and we can remove the uncharged sphere
on the opposite side). The second is to raise the central
sphere so that it is above the ring, but still on its axis of rotation.
This animation shows the result. Here the whole system has
been rotated 90 degrees.
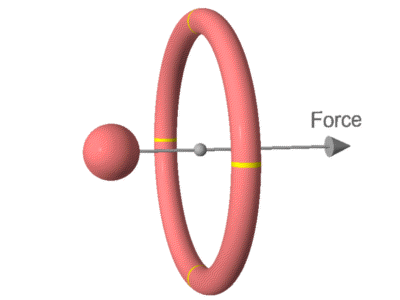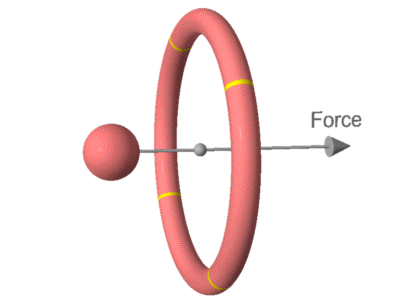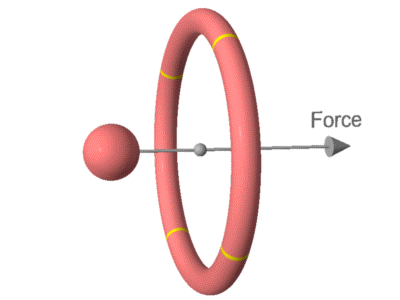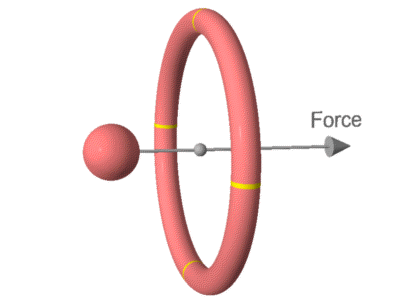
Looking at the diagram, the electric field that emits from the rotating
ring will need to originate at a slight angle (opposite to the
direction of rotation) in order to hit the sphere. As a
result it will hit the sphere at a speed below c and exert less
force. The faster the rotation, the greater the angle will be
required, and the less the impacting field speed and force.
Whereas the field that comes from the sphere will impact the ring at
speed c, and exert full force. As a result the forces will be
unequal and there will be a net force toward the right, causing the
system to accelerate in that direction.
To appreciate this better, imagine that the ring were rotating at the
speed of light. Obviously this can’t be done in
practice! But this is like the earlier example where the
carousel was rotating at the same speed as the balls were
thrown. In this case none of the field originating from the
ring will be able to hit the sphere, no matter what angle it emits
from. All the electric force will come from the sphere
impacting on the ring, pushing the system to the right.
Doing the calculations
Now comes the interesting part: figuring out just how much force we are
talking about.
There are actually two considerations involved. The first is
the reduced field-speed at impact, as discussed already. The
second is the spreading of field with time.
Going back to our original example, imagine that instead of tennis
balls, the boys had toy shotguns. These guns ejected a spray
of (harmless) pellets that radiated from the end of each barrel in a
uniform conical distribution. The further away the target,
the fewer pellets hit, and the less the force. Also if the
person firing the gun was moving backward at the time, the pellets
would take longer to get there. As a result, they would
spread even wider and the force they applied would be weaker again.
The same principle applies to electric fields emitted from
charges. If the charge is moving away from the target, and
both the source and target have the same charge sign (e.g. both
positive), the target receives less force on account of: 1) the
impacting field speed is reduced, and 2) the field has spread wider.
Experimenting with the sphere’s positioning tells us that the maximum
force will be achieved when the height of the sphere above the ring is
1/squareroot(2) of the ring’s radius, i.e. 71% of the radius, putting
it at a 35 degree elevation (this is what is the animation shows).
The calculation for the net force ends up being rather messy,
containing many square roots and cubes. But it can be
simplified to a convenient ‘first order’ expression [2]:
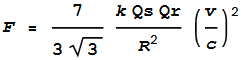 --- (1)
--- (1)
Where:
F = net force
Qs = charge on sphere
Qr = charge on ring
R = large radius of ring
k = Coulomb’s constant
v = velocity of ring
So it would appear we need to: 1) maximise the charge on both the
sphere and ring, 2) maximise the velocity, and 3) minimise the radius.
For a hypothetical setup, we’ll set the radius at 1 metre.
Next we need to make the charge as large as we can. The
sphere could be something that sits atop a Van de Graaff
generator. Looking up what a typical voltage would be on
that, it’s about 450kV. For a sphere of diameter 30cm, that
translates to a charge of 7.5x10-6 C = 7.5 micro-coulombs
[3]. Assume the ring was a hollow tube and also held the same
charge.
We now have all the variables except velocity. We want that
to be as high as possible. That means: make it as high as we
can without having centrifugal force break the ring apart.
This velocity will depend on the strength and density of the
material. Surprisingly, it doesn’t depend on the large radius
of the ring or its cross-sectional thickness. The maximum
velocity you can spin a ring at before it stretches beyond its damage
point turns out to be given by this formula:
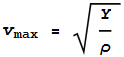 --- (2)
--- (2)
where Y is the yield-strength of the material and ρ is the
density. A table on Wikipedia [4] shows the best conductive
(metallic) candidate is a steel with yield-strength 2617MPa and density
8g/cm3. This gives a maximum rotation speed of 570m/s.
Plugging those numbers in to our force equation gives us... 2.5x10-12 N
2.5 pico-Newtons!? That’s nothing to get excited about and
might not even be measureable, even in zero gravity. Given
that we are violating Newton’s force laws we shouldn’t expect anything
that would be easily noticeable.
Still, let’s see what might be done to boost the results.
There are four variables to play with: two charges, radius, and
velocity.
Radius:
We could increase force by reducing radius. By reducing the
radius to 10cm and leaving everything else the same, the force will
increase by a factor of 100, to 250 pN, which is not much
better. Problem is, reducing the radius also reduces the size
and hence the charge of both sphere and ring: If the sphere
and ring are both hollow, they will also both reduce their surface
areas and hence charges each by a factor of 100, making the force 100
times smaller! Scratch that idea. It would be
better to increase the radius and size of the entire setup.
Velocity:
There isn’t much that can be done to increase the rotational velocity
due to centrifugal forces. In fact it’s unlikely we could get
to 570m/s because the ring would need to be perfectly
balanced. 300m/s might be more realistic. But if stability
wasn’t a problem, we could surround our conducting ring with a layer
of higher-strength/lower-density material. Referring to this
table [4] and equation (2), Kevlar would allow for
speeds up to 1585m/s, boosting the force 7.7 times.
Charge:
The charge on the sphere and ring was very small, in the order of
micro-coulombs. Multiplying these together is what made put
result in the pico (10-12) range. If it were possible for
both the sphere and ring to contain one coulomb of charge, the force
would be 0.04N. Now that is certainly noticeable.
The problem is that we can’t have an isolated charge that
high. The repulsive force between the sphere and ring would
be 4 billion Newtons! That is too much to ask for, but if we
could somehow have each of them contain a milli-coulomb, that force
would reduce to a ton, which is manageable, but then the force within
the sphere might be too high to contain.
Using superconductors
There may be a way around the tiny charge problem. It
involves superconductors. A superconducting ring allows
electrons to circle endlessly. How fast will they move, and
more importantly, how much moving charge will there be?
Suppose the ring was solid copper with a cross-sectional radius of
3cm. This gives it a volume of 0.0178m3. We know
the free electron density of copper is 8.48x1028 electrons per
m3. Multiplying by the charge of an electron gives a charge
density of 1.36x1010 coulombs per m3. Multiplying this by
volume tells us the circling charge will be 2.41x108
coulombs. That’s impressive!
Now how fast will the electrons be moving? Superconductors
can carry a current of 2000 amps per square millimetre of
cross-sectional wire. The velocity can be given by the
formula v=I/(ρ A). Where I is current, ρ is charge
density, and A is area. Substituting I=2000, ρ=1.36x1010,
and A=10-6m2, gives the velocity of 0.147m/s - about 15cm/s.
A small problem here is that circling charge is now negative rather
than positive, because it consists of electrons, and we want the ring
and sphere to have the same polarity. This could be solved by
making the sphere negative. But as will be discussed in the
next section, a positive charge is preferred.
Another way to solve it is by rotating the ring in the opposite
direction. I.e. if the electrons were going clockwise, we
rotate the ring anticlockwise at the same speed (15cm/s). In
this way the electrons are effectively standing still while the protons
are orbiting.
Plugging this new charge (of the ring) and velocity into the above
equations tells us the net force is 5.26x10-6N or 5.26 micro-Newtons.
That is a lot larger. Not enough to be useful but it should
be detectable.
The reason it was much larger was because the charge increased
significantly. At the same time however, velocity greatly
decreased. This had a big impact because the force is
proportional to velocity-squared.
So what can be done? One possibility would be to find a way
of increasing the sphere’s charge. The sphere carried only
7.5 micro-coulombs. It was hollow, which means charge could
only be applied to the surface. What if the sphere were solid
metal – could it hold a much larger charge? Perhaps not
because otherwise it would be standard fare to make Van de Graaff
generators with small solid balls rather than large hollow
spheres. Quite likely this is because once the positive
charge density reaches a certain level it won’t allow any further
electrons to be pulled away by the charging belt, and the charging
process stops. This is probably why they use a large hollow
sphere to spread the charge over a large area.
Here’s a few ideas:
. Use a series of hollow spheres of increasing size. Charge
them separately, then disassemble them into hemispheres, then
reassemble them so they are one inside the other. Could that
boost the overall charge?
. Have a long rectangular sheet of flexible metal. Charge it
as much as possible, disconnect it from the generator, then roll it up
like foil. Now the charge should be confined within a small
volume.
. A limitation to the maximum voltage on Van de Graaff spheres appears
to be that electrons can leak into, or be absorbed from, the
surrounding air. What if we covered the metallic surface with a
dielectric material such as what is used in capacitors. Would
that allow for a much higher voltage/charge? A simple vacuum
might even be better.
Using opposite charges?
Up until now we’ve had using the same charge on the ring and sphere
(both positive). What would happen if they were oppositely
charged: e.g. the sphere was negative and the ring positive?
That would seem more sensible because the net charge of the system
would be neutral.
In this situation you might expect the net force would now be to the
left. Surprisingly this is not the case: the net force is
still to the right. The field from the positive ring would
arrive at the negative sphere at less than light speed, making it’s
attractive force stronger, while the attractive force from the sphere
on the ring has normal strength.
But the net force won’t be as strong. The radiating aspect of
the field also serves to make the attraction (from the ring)
weaker. Doing the analysis gives this first-order
approximation:
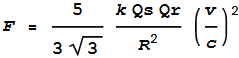 --- (3)
--- (3)
The difference between this and the earlier equation (1) is a factor of
5/7.
One reason for preferring positive charge is that it doesn’t move
around. Negative charge comes from excess electrons, which
are free to move about and this might negate the benefits.
Also, positive is preferred because excess electrons can more easily
leak away or be ejected, discharging the apparatus. Whereas
excess protons can’t leave.
Rotating faster than the current
The fact that both negative and positive rings produce a net force in
the same direction (although by different amounts) could well be the
huge bonus we’re after.
Earlier we rotated our superconducting ring in a direction opposite to
the electron current to make the protons orbit instead. What
if we rotated our ring faster than 15cm/s, i.e. faster than what the
electrons moved through the ring?
Both protons and electrons would now be orbiting in the same direction,
with the protons moving faster. Both charge types would be
contributing to the net force, making it stronger again. The
new net force (adding formulas (1) and (3)) becomes:
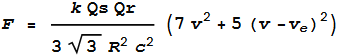 --- (4)
--- (4)
Where:
v is the rotational speed of the ring
ve is the velocity of the electrons relative to the ring, in this case
0.147m/s
By rotating the ring at 1m/s the net force becomes 0.00037N.
By rotating at 10m/s it becomes 0.041N. Rotating at 100m/s
gives 4.2N. And at 300m/s gives 38N.
These are certainly noticeable forces, and actually usable.
38 Newtons can accelerate a 3.8kg mass at 1 G.
The benefit of rotating the superconductor as a whole is that we don’t
need to care so much about how fast the current is flowing, because our
rotation speed will be much greater. So we can use cheaper
superconducting materials that don’t allow huge currents. We
can probably also use regular conductors (e.g. copper wire
electromagnets), although these will need to be kept powered by an
electrical supply.
Either way, it is important to keep some kind of current flowing within
the ring, otherwise the free electrons might move in a manner that
negates the effects, meaning that a neutral spinning disc won’t achieve
anything. For the same reason, it may be necessary to keep a
net charge on the sphere.
Closing thoughts
If the above is correct then why hasn’t it been noticed
before? Perhaps it has. There is a fellow by the
name of Eugene Podkletnov who claimed to have discovered an
‘antigravity’ effect using a rotating superconducting disc.
There are few details available and, amidst much controversy,
counter-claims and denials, it is generally dismissed by the scientific
community as erroneous. But if there’s truth to it, it might
be that he was using a method similar to the above without
understanding why it worked.
This article gives general information:
archive.wired.com/wired/archive/6.03/antigravity_pr.html
This snippet is of interest:
“We found that any object above the disc lost some of its weight, and
we found that if we rotated the disc the effect was
increased.” (emphasis added)
This is in line with what is being described here. Could it
be that the object had a slight charge? What would happen if
they replaced it with something highly-charged?
If anyone has the necessary equipment and materials to try this out,
feel free to do so!
[1] By comparison, Earth-bound vehicles are not limited by ejectable
mass but available energy. An electric car will come to a
stop when its batteries are used up. But a spacecraft without
propellant has no control over its trajectory, no matter how much
electricity can be drawn from its solar panels.
[2] The full expression is here. Replace v with
v/c. It works for any charge signs (+/-).
[3] The voltage/charge relationship is given by the relationship V = k
Q/r, where r is the sphere’s radius – 0.15m in this case.
[4] http://en.wikipedia.org/wiki/Ultimate_tensile_strength
|



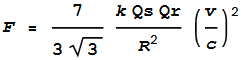 --- (1)
--- (1)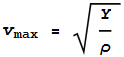 --- (2)
--- (2)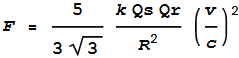 --- (3)
--- (3)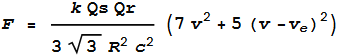 --- (4)
--- (4)