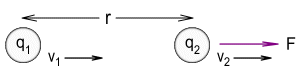Alternatives to Relativistic Mass

Special Relativity (SR) tells us that objects should increase in mass as they get faster. When at rest relative to an observer, an object has a fixed mass, called ‘rest mass’. As the object increases its speed relative to the observer, it will become steadily heavier. And as it approaches the speed of light the mass will become infinite.

This is called relativistic mass (RM). The degree of mass increase will be in accordance with the Lorentz Transform (LT). The effect of RM is to slow the acceleration of an object and prevent it from reaching light speed. For example suppose we have the following setup:

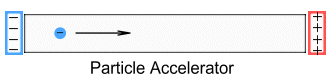
A simple particle accelerator (shown above) is constructed by placing two electrically charged plates at either side of a vacuum tube. Inside the tube is a single electron. Initially the plates are neutral and the electron is at rest. When a voltage is applied to the plates this creates a uniform electrical field inside the tube. This field then applies a force to the electron which causes it accelerate. The extent of acceleration can be calculated using factors of mass, charge and voltage.

According to SR, as the speed of the electron approaches the speed of light, its mass will become increasingly greater and this will inhibit further acceleration. As a result the electron will never quite reach light speed because to do so would require accelerating an infinite mass.

Unlike the problems earlier presented with time dilation and length contraction, RM contains no inherent contradictions. For example an increase in the electron’s mass relative to the accelerator should also require a corresponding increase in the mass of the accelerator relative to the electron. But since the accelerator is already vastly heavier than the electron it makes no difference whether its mass increases or not; i.e. it already has enough inertia to resist the recoil of a heavier electron.

Mass vs. Charge

Assuming that experimental evidence is correct in confirming a decrease in acceleration as particles move towards light speed, might there be other ways of explaining this phenomenon, other than by suggesting a mass increase? While it is true that an increase in mass would certainly slow the rate of acceleration, it is also true that a decrease in charge could achieve the same. In other words, suppose that as a particle increased in speed, its electrical charge steadily decreased toward, and became zero at light speed. In this situation, the amount of electrical force experienced by the particle would decrease, and this would slow acceleration. The end result would be the same – a light-speed limit.

This concept of charge-decrease has a distinct advantage over the concept of mass-increase: It is far easier to imagine zero charge than it is to imagine infinite mass. Infinites can’t exist in nature, whereas ‘zeros’ can.

This is not to suggest that charge-decrease is the correct explanation since there is no particular reason why either phenomenon should occur. Instead I would like to present a different explanation for the phenomenon of acceleration decrease that is more in-line with classical mechanics and common sense.

The Wind Tunnel

Imagine a wind tunnel such as that shown below. It has fans at both ends to ensure a smooth flow of air at constant speed along its length. The fans are initially off. At one end of the tunnel is a marble. The marble sits in the cross-sectional centre of the tunnel so we’ll need to imagine that this is a zero gravity environment or that the marble is somehow magnetically suspended away from the tunnel walls.

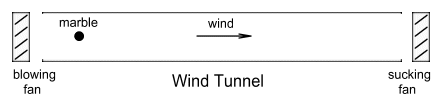
Now let’s turn on the fans. Very quickly the air in the tunnel accelerates to a constant velocity as determined by the fan speed. This moving air applies a force on the marble which then accelerates. Under the constant influence of this force the marble moves increasingly faster along the tunnel.

What happens as the marble approaches the speed of the wind? The acceleration slows down. As the marble approaches the wind speed the acceleration decreases because the relative speed of the wind on the marble becomes ever smaller. The net result is that the marble will become ever closer to the wind speed but, in theory, never quite reach it.

So why did the marble slow down is it approached wind speed? Was it because its mass increased toward infinity as it neared wind speed? Of course not! The reason it slowed down is that the force on the marble was decreasing as the wind speed relative to the marble decreased. Once it reached wind speed there was no more force and therefore no more acceleration.

Well, I’m going to suggest that the electron in the earlier example slowed its acceleration for much the same reason. As you can see this wind tunnel is analogous to the particle accelerator. Simply replace ‘wind tunnel’ with ‘particle accelerator’; ‘marble’ with ‘electron’; ‘fans’ with ‘charged plates’; and ‘wind’ with ‘electric field’.

A static electric field is just light – light with zero frequency. It emerges from the plates at exactly light speed. It exerts a force on the electron, initially at light speed. Does it not make sense to say that this force should decrease as the speed difference between the electron and the field decreases? And if the electron is moving away from the field at the same speed that the field is approaching it, then how could the field possibly exert any force on it? It is difficult to imagine how it could.

Here’s a better example: Imagine that the accelerator had just been switched on and the electron was already moving away from the negative plate at light speed. Well, the field would be chasing a moving target and could never reach the electron; therefore it could not possibly apply any force to the electron.

Speed Differencing

I submit therefore that the real reason for a particle’s slowdown near light-speed has nothing to do with an increase in mass, and everything to do with a decrease in force that results from a difference between field speed and particle speed. Of course it is also possible that an increase in mass could be responsible for the same result. But why invent a complicated reason to explain a phenomenon when a more plausible explanation is available?

Assuming I’m right here, how exactly should the force vary with a particle’s speed? We are a looking for a function that decreases towards zero as v moves towards c. The LT does this, or rather 1/LT does, but there are also other possibilities to choose from. In the case of the wind tunnel, the force F on the marble is proportional to the square of the difference between wind speed and marble speed. This is a function of fluid dynamics. I am going to suggest that an electric field acts on an electron in much the same way, except that it works according to the cube of the difference. Namely:

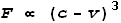
$F \propto (c-v)^3$

Why the cube and not the square? There’s a subtle difference and the reason will be explained in a later chapter about magnetism.

This equation shows a proportional sign so it cannot be directly used as a multiplier. What we want is a function that can be applied to a regular force equation. The function needs to have a value of one at v=0 and a value of zero at v=c. This can by easily done by dividing by c. I.e.:

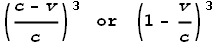
$\left(\frac{c-v}{c}\right)^3\text{ }\text{or}\text{ }\left(1-\frac{v}{c}\right)^3$

For the sake of giving this a name I’ll call this the Electric Velocity Force Function (EVFF). If applied to a force equation it could look like this:

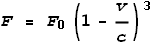
$F = F_0 \left(1-\frac{v}{c}\right)^3$

Where F₀ is the force at zero velocity, and F is the ‘relativistic’ force.

Interactions between opposite charges

The above formula can be used when determining the interaction between ‘like’ charges; i.e. both negative or both positive. Now let’s consider interactions between opposite charges.

Opposite charges interact the other way around, in that their force will decrease as they move faster together. To understand this, refer to the wind tunnel example. The fan on the left is blowing the marble while the fan on the right is sucking. As the marble moves faster away from the blowing fan, the force from that fan decreases. Likewise as the marble moves faster toward the sucking fan, the force from that fan decreases. In our analogy, the blowing fan is the plate with negative charge (same as the electron) and the sucking fan is the positive plate (opposite of the electron).

So in the case with opposite charges, the EVFF becomes:

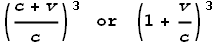
$\left(\frac{c+v}{c}\right)^3\text{ }\text{or}\text{ }\left(1+\frac{v}{c}\right)^3$

The sign in front of the velocity becomes positive, not because velocity has changed direction, but because the charges are opposite.

A Velocity Dependent Coulomb’s Law

Now let’s create a variation of Coulomb’s Law that takes into account particle velocities. Coulomb’s Law tells us the amount of electrical force that exists between two charged particles a given distance apart. The equation for this law is:

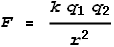
$F = \frac{k q_1 q_2}{r^2}$

Where F is the force experienced by both particles, k is Coulomb’s constant, q₁ and q₂ are the charges of particles 1 and 2 respectively and r is the distance between them.

This formula is considered true for static charges. Next we’ll introduce what I’ll call the ‘Velocity Dependent Coulomb’s Law’ (VDCL) which allows for moving charges. Consider the below diagram that shows moving charges:

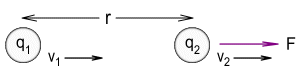
The modified force equation for this situation becomes:

$F = \frac{k q_1 q_2}{r^2}\left.(1+\frac{\left[q_1\right]\left[q_1\right] \left(v_1-v_2\right)}{c}\right){}^3$

Where F is the force experienced by particle 2, v₁ and v₂ represent the velocities of particles 1 and 2 respectively and r is the distance between them. The term [q₁] refers to the sign of charge q₁; i.e. for a positive charge like a proton [q₁] = +1 and for a negative charge like an electron [q₁] = -1. Likewise [q₂] is the sign of charge q₂.

[Sidenote: To be precise, v₁ is not the current velocity of particle 1 but the velocity particle 1 had when it generated the field that has now reached particle 2. This is a subtle distinction because there is a brief delay between when particle 1 emits its field and when that field reaches particle 2; and the velocity of particle 1 could change during that time. This will be covered later in more detail.]

So why not just use the conventional LT instead of the EVFF? I discussed in an earlier chapter that the LT is based on questionable assumptions about time dilation that, even if true, shouldn’t apply to one-dimensional situations such as this. Of course it’s still possible that the regular LT may be the correct function.

The above equation however does have some large benefits. If we assume it to be correct then a number of physical phenomena can be neatly explained including magnetism and static electricity as I will show in the following chapters.

Examples with Same charge

Below are some diagrams to better describe this. In each of these examples particle 1 is at rest and particle 2’s velocity is given by v. I.e. v₁ =0 and v₂ = v.

First we have two positively charged particles at rest. Let’s say they are placed fixed distance apart and each experience an opposing force of 1 Newton (see below).

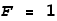
Now we will repeat the above but this time they are moving away from each other with a speed of c/2 (half light speed). When they are the same distance apart what will the force be?

According to the EVFF,

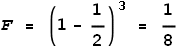
$F = \left.(1-\frac{1}{2}\right)^3 = \frac{1}{8}$

So they experience an opposing force of 0.125 Newton; a large decrease when compared to the static situation.

Now to repeat the above but this time they are moving toward each other with a speed of c/2 (half light speed). When they are the same distance apart what will the force be?

The EVFF describes a positive velocity as moving away. So the velocity here is -1/2 and EVFF shows:

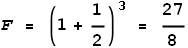
$F = \left.(1+\frac{1}{2}\right)^3 = \frac{27}{8}$

So they experience an opposing force of 3.375 Newton. Here the force has greatly increased.

Examples with Opposite charge

Take two identical but opposite charges, initially static and the same distance apart as in the above examples. They will each experience an attractive force of 1 Newton.

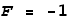
Now we will repeat the above but this time they are moving away from each other with a speed of c/2. When they are the same distance apart what will the force be?

The equation is the same as for similar charges but the force direction is different. According to the EVFF,

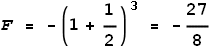
$F = -\left(1+\frac{1}{2}\right)^3 = -\frac{27}{8}$

So they experience an attractive force of 3.375 Newton; an increase when compared to the static situation.

Now to repeat the above but this time they are moving toward each other with a speed of c/2. When they are the same distance apart what will the force be?

Here both the velocity and the charge are negative and EVFF shows:

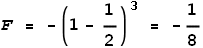
$F = -\left.(1-\frac{1}{2}\right)^3 = -\frac{1}{8}$

So they experience an attractive force of 0.125 Newton. Here the force has decreased and this retards the rate of acceleration.

Conclusion

It is possible to explain the decrease in acceleration of an object near light-speed without requiring a mass increase toward infinity as it approaches light-speed. One method is to say that the force of an electric field on a charged particle is proportional to the difference between field and object velocities. This is similar to the way fluid forces behave in classical mechanics.