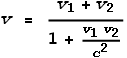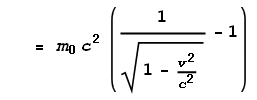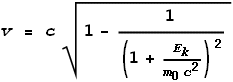Faster Than Light Travel
Any in-depth discussion of Special Relativity (SR) frequently raises the question:
“Is it possible to travel faster than the speed of light?”
To this question SR always responds with an emphatic “NO”. SR is largely
built on the premise that light is the universal speed limit, and throws up many roadblocks
that thwart any attempt toward achieving Faster than Light (FTL) speeds, or even reaching
light speed.
Firstly SR tells us that if you try to accelerate an object to light speed, its mass will
increase toward infinity, preventing further acceleration. Secondly it tells us that the
apparent distance between object and observer decreases near light speed, and this reduces
the calculated speed. And thirdly it tells us that experience of time will be different
between object and observer, which may further invalidate speed calculations.
With so many obstructions in our path it appears that FTL is quite impossible. And so it
would be – providing you accept SR’s premises as being true.
In earlier chapters I presented a number of logical contradictions existent within the time dilation and length
contraction premises. I further showed an alternative explanation to the phenomenon of
relativistic mass, that did not require an increase in
mass. In other words it is possible that SR’s premises are incorrect.
Returning to the question of “Is it possible to travel faster than the speed of
light?” I will answer “Yes”, but with a caveat. In the previous section on relativistic mass I suggested that the slowdown of
particles near light speed may be due to an electric field having less force as a particle
approaches the field speed. So a particle moving at field speed could not move faster than
light because the light (the electric field) can no longer apply pressure to it.
Let’s use a gun as an example. When a gun fires a bullet, the bullet is propelled by
a force from the explosion of its propellent. The explosion is a chemical reaction that
produces rapidly expanding gas. The final speed of the bullet is determined partly by the
masses of both bullet and gas, but mainly by the speed of the gas. In other words, the
bullet is limited by the speed of the gas expansion. Using a higher powered explosive will
produce a higher expansion speed, and thus a higher bullet speed, but ultimately the
bullet’s speed is limited by the rate of gas expansion.
Analogous to an electron in a particle accelerator; the electron is the bullet and the
field is the expanding gas. In other words the reason the electron won’t exceed light
speed is not because it has hit a universal speed limit but because the speed of its
propulsion, the electric field, is limited.
Going beyond light speed
So if an object, e.g. the electron in our accelerator, cannot even
accelerate to light speed, then how could it ever get past light speed? Consider the
bullet from the above example. A typical speed for a bullet from a handgun is 800m/s. For
a high power rifle the speed can be 1500 m/s [1]. Now consider the
speed of a man-made satellite, such as the International Space Station (ISS). The ISS
orbits the Earth at a speed of 7680 m/s [2]. The ISS was not originally
at this speed: it was in pieces on Earth and the fastest it was moving was that of the
equator, about 460 m/s, making the speed difference 7220 m/s. If you can’t get a
light-weight bullet beyond 1500 m/s then how could you get a much heavier ISS to 7220 m/s?
The answer of course is to do it in stages. The rifle uses one almighty push to accelerate
the bullet to top speed; expending the full chemical energy of its explosive propellant in
one instant. Satellites instead use a rocket that releases its energy over a period. Each
increment of fuel burned causes acceleration of the rocket. The net result is a higher
speed.
We should therefore be able to employ a similar method to get beyond light speed.
Providing we have enough fuel for our rocket it should in theory continue in its
acceleration beyond light speed. The rocket exhaust would leave the rocket at speeds much
less than light, relative to the rocket itself. So at no time would anything need to move
beyond light speed relative to its source. The practicalities of building such a ship are
another matter entirely. Here we are interested only in possibilities.
A different take on relativity speed limits
If my earlier arguments about time dilation and relativistic mass are
correct, I would like to propose a different theory regarding motion:
Replace: “No object can exceed the speed of light” with:
No object can exceed the speed of light relative to its launch point.
In other words the speed of light is limited, but the speed of a material object is not.
An electromagnetic field moves at a fixed speed (c) relative to the
charge that is producing that field. This limits the speed of a particle that the field
may accelerate but doesn’t prevent that particle from being further accelerated at a
later stage by a different field.
‘Launch point’ refers to what is providing the force. In the case of the
electron it’s the charged plates. For the bullet it’s the propellant and casing.
And for the rocket it’s the fuel and jets. So for the rocket, its launch point is not
the Earth. The Earth is merely the starting point of its journey. The Earth does not
provide any ‘push’ to accelerate the rocket and therefore cannot be a limiting
factor to the ultimate speed of the rocket.
Additive velocities
SR also contends that velocities cannot be added together in the same way
as they are in classical mechanics. For example if two objects move in opposite directions
both at speed 0.8c from a common starting point, classical mechanics
tells us that their velocity relative to each other should be 1.6c –
60% faster than light.
SR however uses a different formula namely:
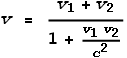
Where v is the observed velocity and v1
and v2 are the velocities of particles 1 and 2 and are in
opposite directions. I will leave out the derivation of this formula; suffice to say that
it comes from the time dilation and length contraction formulas, both of which come from
the Lorentz Transform (LT). In our example above, v1 and v2
are both 0.8c, so the observed velocity will be 0.976c,
which is less than light. The formula guarantees that v<c.
An obvious problem here is the phrase ‘observed velocity’ which implies that we
don’t know how fast an object is travelling, but from the point of view of each
particle, it looks like the other is travelling at less than light speed. This is
misleading because we should not care what a speed looks like, only what it is.
It is also highly doubtful that it ‘looks’ like anything because the light from
a source moving away from an observer at faster than light speed could not reach the
observer.
The lonely astronaut
To overcome the confusion of appearance in velocities we need to set up an
experiment that removes the need to see a particle. This can be done with a ‘round
trip’ situation, which involves having a particle travel a known distance and then
return. In this way we can easily calculate the average speed of the journey.
Suppose that a planet is discovered exactly at one light year away from Earth. Scientists
decide to send an astronaut there; which they somehow manage to do. Once there the
astronaut needs to communicate with Earth. Suppose that Earth sends a message via a laser
pulse and immediately upon receiving this, the astronaut sends a reply using another
laser. How long will it take to get the reply? Answer: two years – a year there, plus
another year back.
Now suppose a special bullet exists that can carry messages. This bullet is very special
in that it can travel up to 99% of light speed. Once at that speed the bullet will fire a
secondary bullet that can also travel at 0.99c, relative to the first
bullet. The astronaut also has a supply of similar bullets. So Earth fires a bullet that
leaves their gun at 0.99c. Once the bullet has escaped Earth’s
gravity, it then fires its secondary bullet that moves at 0.99c relative
to the first bullet. The message in the secondary bullet arrives and the astronaut quickly
replies using one of his own bullets. How long will it take to get the reply? Answer:
logically speaking, just over one year – half a year there, plus another half back.
SR proponents might argue that, due to additive velocities, the secondary bullet will only
appear to travel at 0.99995c, relative to Earth. But it is not important
how fast either bullet appears to move because the round trip makes appearances
irrelevant. The message has travelled a distance of two light years in the time of just
one year and therefore has done so at twice light speed.
The rotating disk
Here’s another approach.
Suppose we had a very large disk floating in space, and with a radius equal to our
Earth-Moon distance. We decide to apply a steady turning force (a torque) to its inner
region. There are a number of ways of doing this. One method is to have another disk
underneath rotating in the opposite direction. Another is to attach a set of
sideways-angled rockets to the inner region. We’ll choose the second. What will
happen?
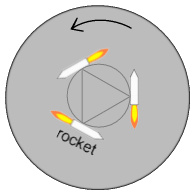
The disk is very massive so initially we shouldn’t expect much other than
some internal flexing. But providing we keep the force constant, at some point the disk
must begin to rotate as a whole.
When the disk is rotating once every 28 days, the rim of the disk will be moving as fast
as our Moon does – about 1000 m/s. Assume we have an almost unlimited supply of rocket
fuel. Providing we keep the force constant the disk should steadily rotate faster and
faster.
When the disk rotates once a day its rim will be moving at 28 km/s. When it rotates once
per hour, 672 km/s. Once per minute: 40 thousand km/s, which is 13% of light speed. If
the disk makes it to one rotation every 8 seconds the rim will be moving at light speed.
And if it rotates once per 4 seconds it will be going at double light speed. Providing
the disk is strong enough to save it from flying apart, is there anything in SR to
prevent this?
SR proponents would argue that once the rotation approaches 1/8th per second, the rim
will become infinitely massive and the rockets would be unable to push it any faster. But
the rockets aren’t pushing the outer rim. The outer rim is being pushed by the inner
rim, which is being pushed by the region just before it, and so forth, all the way back
to the rockets. The speed difference between the outer and inner rims is much less than
light speed and will therefore be unaffected by relativistic mass considerations. Hence
there is nothing in SR to prevent the outer rim from being pushed beyond light speed
relative to the rockets.
Breaking FTL on a microscopic scale
There is a much easier way to break the light speed barrier; and one that
probably occurs on a regular basis with charged particles. Consider these different
arrangements of electrons:
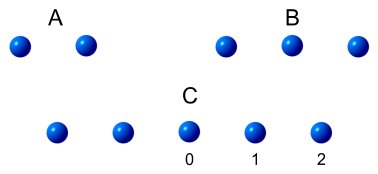
The first example (A) shows two electrons held close together. There is a
large opposing force between them and they would quickly fly apart if let go. As they move
apart, the force between them decreases. Classical mechanics tells us that the force
between them will always be greater than zero, no matter how far apart they are, and
therefore the electrons should move toward an infinite speed. But SR will say that their
mass will increase and keep speeds less than light. So at this point FTL has not been
achieved and we move to the next example...
Example B shows three electrons held in a straight line with equal spacing. When released,
the middle electron will remain stationary because it is at the exact mid-point and the
outer electrons will fly apart. SR will say that each of the outer electrons will
accelerate toward light speed relative to the electron in the middle. Arguably then, the
outer electrons are now travelling at nearly twice light speed relative to each other and
we have broken the speed barrier.
Opponents of this argument might point out that, while it appears that the outer electrons
are moving at FTL relative to each other, neither is moving FTL relative to their starting
point. So the barrier hasn’t been broken after all. This is certainly true. One
of the reasons for wanting FTL is for communications and this situation doesn’t help
with that. Two couriers running in opposite directions can’t deliver a parcel any
faster. So we move to the next example...
Example C shows five electrons held in a straight line with equal spacing. When released,
the middle electron will remain motionless; but this time the situation for the other
electrons is different. Looking at the numbering in the above diagram, if the middle
electron is number 0, then SR tells us that electron 1 must eventually accelerate to near
light speed relative to 0. Likewise electron 2 must accelerate to near light speed
relative to 1. So electron 2 is now travelling at nearly double light speed relative to
its starting point.
We could expand on this idea using 7, 9 and 11 electrons to achieve speeds of 3, 4 and 5
times light speed respectively. Every electron feels a force from all the others, but due
to the distances, the primary force will be from the nearest electrons. SR has not been
violated because no electron is moving at FTL from its neighbour. In the practical sense
of a three-dimensional world, this would be done by somehow forcing a bunch of
like-charged particles into a tight ball then releasing them.
Experimental Evidence for FTL
Having speculated on the possibilities, we should now investigate what
evidence may be available to support FTL travel. Here we are concerned with particles
rather than light waves. We know that doing this in a laboratory as a multi-stage
acceleration is going to be difficult. So let’s look elsewhere: to outer space.
Some years ago I read a newspaper article about the FTL question. Apparently scientists
had discovered some high speed protons that were expelled as cosmic rays from a supernova.
The protons were measured to be travelling at something like 0.9999993c.
It was the fastest speed ever recorded for a material object and importantly, was just
less than light speed.
This struck me as impressive evidence for the universal speed limit. And yet I wondered
how it was that they could make their measurements so accurate. After all, a small yet
legitimate measurement error could have easily given the result as 1.0000003c
instead, which would still be valid evidence for a light speed limitation. A number of
similar experiments [3] curiously yield the same result: the measured
speed is always just under, and never greater, than c. Is this just
coincidence or is there something else going on?
Normally to measure speed you would time how long an object took to travel a known
distance, which is basically the definition of speed. It so happens that when measuring
the speed of atomic particles, it’s not done that way. Protons are basically
invisible, so the method used is to measure the energy of their impact, then to calculate
their velocity based on energy and mass. Calculating velocity from energy is a perfectly
good method. In classical mechanics, the speed of a particle of known mass and kinetic
energy can be calculated from the trusty E=½mv2 formula.
E.g. a particle of mass 1 kg and energy 8 joules must have a velocity of 4 m/s.
Well SR is a whole different ball game. Everyone knows you can’t use the classical
mechanics energy formula near light speeds. Instead you must use the E=mc2
formula and deduct the rest energy E0 from the total energy E.
For a particle of rest mass m0 having kinetic energy Ek,
this is what you must use:
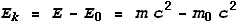
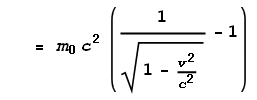
For low velocities this will approximate to the classical kinetic energy
equation. What we want here is the velocity component, which can be extracted as:
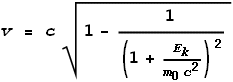
If you consider this equation carefully you’ll notice that for all
positive values of Ek and m0, the
term inside the square root must always be less than 1. Therefore v must
always be less than c. Using this calculation there is no possibility of
velocity ever exceeding light speed!
What has happened here? A series of steps starting with the assumption that velocity must
always be less than light has led to equations that were then used in calculations to
prove the original assumption. The LT appears in the equation to convert relativistic mass
and this is the term that limits velocity to light speed.
This is total nonsense. It doesn’t prove that v<c;
it only assumes it and then forces the assumption via an equation based on that
assumption. Here is the logic involved:
1. Scientists postulate that light is the ultimate speed.
2. From this the LT is derived, and the relativistic energy equation E=mc2
follows from the LT.
3. Scientists then search for evidence to test the postulate.
4. High energy particles are found.
5. Relativistic energy equation is used to calculate velocity of the particles.
6. The equations prove the postulate that they were based on.
Basically the LT has been used to verify itself and the only thing it confirms is that
LT=LT. A proof cannot be based on an assumption; it must be based on confirmed facts. If
the classical mechanics energy equation had been used instead, a very different speed
would have been calculated [4].
Time dilation in Muons as Proof for FTL?
In an earlier chapter we looked
at the decay of muons as proof for time dilation. Experimental evidence showed that muons
moving at 0.995c decayed at one tenth of their normal rate. This was seen
as strong evidence for the existence of time dilation since the reduction in half life
corresponds precisely to what SR would predict for that speed.
Given the arguments in the preceding section I would argue that a fundamental error may
have been made in the calculation of speed that would invalidate the conclusions of the
experiment. Furthermore I would like to use this experiment as evidence of the existence
of FTL speeds. The argument runs as follows:
1. Muons moving at 0.995c had an observed half life 10 times greater than
muons at rest.
2. This exactly corresponds to the prediction of SR that they should experience a time
dilation of factor 10 at that speed, and this proves time dilation has occurred.
3. However time dilation is impossible because there are no fixed frames of reference and
it is not possible to say which muons are ‘at rest’ and which are ‘in
motion’. See this earlier chapter for a full
explanation.
4. Therefore the most likely explanation for the observed degree of decay is that the
calculation of speed was wrong and the muons were in fact travelling ten times the
speed of light.
5. Thus the muon experiment proves FTL travel.
Basically the 0.995c speed was based on an energy calculation rather than
an actual speed measurement, and that calculation assumed v<c.
A more detailed discussion is in this supplemental chapter:
Muons and Relativity (<-- click to read)
Conclusions
Faster than Light travel relative to a fixed starting point is possible.
It cannot be done by applying a force from the starting point but can be done using
multi-stage accelerations.
Measurement of the speed of high energy particles is erroneous because it uses formulas
that presume a light speed limit.
The muon decay experiment used to prove time dilation can be explained by, and used to
prove, FTL travel.
-----------------
[1] Bullet speeds: http://hypertextbook.com/facts/1999/MariaPereyra.shtml
[2] Orbit speeds: http://www.freemars.org/jeff/speed/index.htm
[3] I’m unable to find the original article, however it appears
that faster protons have since been discovered. http://www.fourmilab.ch/documents/ohmygodpart.html
puts their speed at 0.9999999999999999999999951c.
This site http://helios.gsfc.nasa.gov/qa_cr.html#crvel
says cosmic rays can move at 0.999999999999c.
The wikipedia entry http://en.wikipedia.org/wiki/Ultra-high-energy_cosmic_ray says the
speed is (1-5x10-24)c but is unsure if the particle was a
proton.
[4] It will left to the reader to calculate the amazing speeds involved! |